Advertisements
Advertisements
प्रश्न
How much paper of each shade is needed to make a kite given in the following figure, in which ABCD is a square with diagonal 44 cm.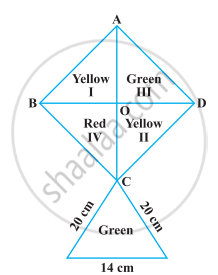
उत्तर
We know that, all the sides of a square are always equal.
i.e., AB = BC = CD = DA
In ΔACD, AC = 44 cm, ∠D = 90°
Using Pythagoras theorem in ΔACD,
AC2 = AD2 + DC2
⇒ 442 = AD2 + AD2 ...[∵ DC = AD]
⇒ 2AD2 = 44 × 44
⇒ AD2 = 22 × 44
⇒ AD = `sqrt(22 xx 44)` ...[Taking positive square root because length is always positive]
⇒ AD = `sqrt(2 xx 11 xx 4 xx 11)`
⇒ AD = `22sqrt(2)` cm
So, AB = BC = CD = DA = `22sqrt(2)` cm
∴ Area of square ABCD = Side × Side
= `22sqrt(2) xx 22sqrt(2)`
= 968 cm2
∴ Area of the red portion = `968/4` = 242 cm2 ...[Since, area of square is divided into four parts]
Now, area of the green portion = `968/4` = 242 cm2
Area of the yellow portion = `968/2` = 484 cm2
In ΔPCQ, side PC = a = 20 cm, CQ = b = 20 cm and PQ = c = 14 cm
`s = (a + b + c)/2`
= `(20 + 20 + 14)/2`
= `54/2`
= 27 cm
∴ Area of ΔPCQ = `sqrt(s(s - a)(s - b)(s - c))` ...[By Heron’s formula]
= `sqrt(27(27 - 20)(27 - 20)(27 - 14))`
= `sqrt(27 xx 7 xx 7 xx 13)`
= `sqrt(3 xx 3 xx 3 xx 7 xx 7 xx 13)`
= `21sqrt(39)`
= 21 × 6.24
= 131.04 cm2
∴ Total area of the green portion = (242 + 131.04) = 373.04 cm2
Hence, the paper required for each shade to make a kite is red paper 242 cm2, yellow paper 484 cm2 and green paper 373.04 cm2.
APPEARS IN
संबंधित प्रश्न
The lengths of the sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side.
Find the areas of the given plot. (All measures are in metres.)
Find the area of the triangle formed by the points
(–10, –4), (–8, –1) and (–3, –5)
Determine whether the sets of points are collinear?
`(-1/2, 3), (-5, 6) and (-8, 8)`
Determine whether the sets of points are collinear?
(a, b + c), (b, c + a) and (c, a + b)
A triangular shaped glass with vertices at A(– 5, – 4), B(1, 6) and C(7, – 4) has to be painted. If one bucket of paint covers 6 square feet, how many buckets of paint will be required to paint the whole glass, if only one coat of paint is applied
Find the area of triangle AGF
An advertisement board is in the form of an isosceles triangle with perimeter 36 m and each of the equal sides are 13 m. Find the cost of painting it at ₹ 17.50 per square metre.
The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
