Advertisements
Advertisements
प्रश्न
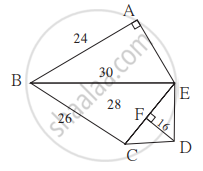
Find the areas of the given plot. (All measures are in metres.)
उत्तर
In ∆ABE, m∠BAE = 90°, l(AB) = 24 m, l(BE) = 30 m
∴ [l(BE)]2 = [l(AB)]2 + [l(AE)]2 …[Pythagoras theorem]
∴ (30)2 = (24)2 + [l(AE)]2
∴ 900 = 576 + [l(AE)]2
∴ [l(AE)]2 = 900 – 576
∴ [l(AE)]2 = 324
∴ l(AE) = `sqrt324`
= 18 m …[Taking square root of both sides]
A(∆ABE) = `(1/2)` x product of sides forming the right angle
= `(1/2) xx l("AE") xx l("AB")`
= `(1/2) xx 18 xx 24`
= 216 sq. m
In ∆BCE, a = 30m, b = 28m, c = 26m
Semiperimeter of ∆BCE,
S = `1/2` (a + b + c)
= `(30 + 28 + 26)/2`
= `84/2`
= 42 m
A (∆BCE) = `sqrt(s(s - a)(s - b)(s - c))`
= `sqrt(42 (42 - 30)(42 - 28)(42 - 26))`
= `sqrt(42 xx 12xx 14 xx 16)`
= `sqrt(6 xx 7 xx 6 xx 2 xx 2 xx 7 xx 8 xx 2)`
= `sqrt(6^2 xx 7^2 xx 8^2)`
= `6 xx 7 xx 8`
= 336 sq. m
In ∆EDC, l(CE) = 28 m, l(DF) = 16 m
A(∆EDC) = `1/2 xx "base" xx "height"`
`1/2 xx l("CE") xx l("DF")`
= `(1/2) xx 28 xx 16`
= 224 sq. m.
∴ Area of plot ABCDE
= A(∆ABE) + A(∆BCE) + A(∆EDC)
= 216 + 336 + 224
= 776 sq. m
∴ The area of the given plot is 776 sq.m.
