Advertisements
Advertisements
प्रश्न
How much paper of each shade is needed to make a kite given in the following figure, in which ABCD is a square with diagonal 44 cm.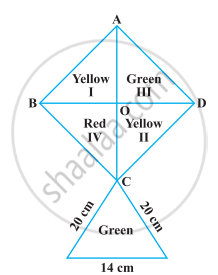
उत्तर
We know that, all the sides of a square are always equal.
i.e., AB = BC = CD = DA
In ΔACD, AC = 44 cm, ∠D = 90°
Using Pythagoras theorem in ΔACD,
AC2 = AD2 + DC2
⇒ 442 = AD2 + AD2 ...[∵ DC = AD]
⇒ 2AD2 = 44 × 44
⇒ AD2 = 22 × 44
⇒ AD = `sqrt(22 xx 44)` ...[Taking positive square root because length is always positive]
⇒ AD = `sqrt(2 xx 11 xx 4 xx 11)`
⇒ AD = `22sqrt(2)` cm
So, AB = BC = CD = DA = `22sqrt(2)` cm
∴ Area of square ABCD = Side × Side
= `22sqrt(2) xx 22sqrt(2)`
= 968 cm2
∴ Area of the red portion = `968/4` = 242 cm2 ...[Since, area of square is divided into four parts]
Now, area of the green portion = `968/4` = 242 cm2
Area of the yellow portion = `968/2` = 484 cm2
In ΔPCQ, side PC = a = 20 cm, CQ = b = 20 cm and PQ = c = 14 cm
`s = (a + b + c)/2`
= `(20 + 20 + 14)/2`
= `54/2`
= 27 cm
∴ Area of ΔPCQ = `sqrt(s(s - a)(s - b)(s - c))` ...[By Heron’s formula]
= `sqrt(27(27 - 20)(27 - 20)(27 - 14))`
= `sqrt(27 xx 7 xx 7 xx 13)`
= `sqrt(3 xx 3 xx 3 xx 7 xx 7 xx 13)`
= `21sqrt(39)`
= 21 × 6.24
= 131.04 cm2
∴ Total area of the green portion = (242 + 131.04) = 373.04 cm2
Hence, the paper required for each shade to make a kite is red paper 242 cm2, yellow paper 484 cm2 and green paper 373.04 cm2.
APPEARS IN
संबंधित प्रश्न
The perimeter of an isosceles triangle is 42 cm and its baše is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
Find the areas of the given plot. (All measures are in metres.)
The area of triangle formed by the points (− 5, 0), (0, – 5) and (5, 0) is
A man walks near a wall, such that the distance between him and the wall is 10 units. Consider the wall to be the Y-axis. The path travelled by the man is
The sides of the triangular ground are 22 m, 120 m and 122 m. Find the area and cost of levelling the ground at the rate of ₹ 20 per m2
Find the area of an equilateral triangle whose perimeter is 180 cm
Find the area of a parallelogram given in figure. Also find the length of the altitude from vertex A on the side DC.
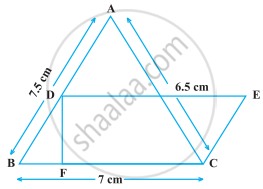
In the following figure, ∆ABC has sides AB = 7.5 cm, AC = 6.5 cm and BC = 7 cm. On base BC a parallelogram DBCE of same area as that of ∆ABC is constructed. Find the height DF of the parallelogram.