Advertisements
Advertisements
प्रश्न
Find the area of the trapezium PQRS with height PQ given in the following figure.
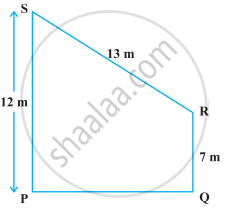
उत्तर
We have, trapezium PQRS, in which draw a line RT perpendicular to PS.
Where, side, ST = PS – TP = 12 – 7 = 5 m. ...[∵ TP = PQ = 7 m]
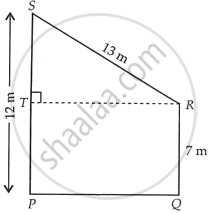
In right angled ΔSTR,
(SR)2 = (ST)2 + (TR)2 ...[By using Pythagoras theorem]
⇒ (13)2 = (5)2 + (TR)2
⇒ (TR)2 = 169 – 25
⇒ (TR)2 = 144
∴ TR = 12 m ...[Taking positive square root because length is always positive]
Now, area of ΔSTR = `1/2 xx TR xx TS` ...[∵ Area of triangle = `1/2` (base × height)]
= `1/2 xx 12 xx 5`
= 30 m2
Now, area of rectangle PQRT = PQ × RQ ...[∵ Area of a rectangle = length × breadth]
= 12 × 7
= 84 m2 ...[∵ PQ = TR = 12 m]
∴ Area of trapezium = Area of ΔSTR + Area of rectangle PQRT
= 30 + 84
= 114 m2
Hence, the area of trapezium is 114 m2.
APPEARS IN
संबंधित प्रश्न
Find the area of the triangle ABC with A(1, −4) and mid-points of sides through A being (2, −1) and (0, −1).
Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
In a ΔABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ΔABC and hence its altitude on AC ?
Show that the points (-3, -3),(3,3) and C (-3 `sqrt(3) , 3 sqrt(3))` are the vertices of an equilateral triangle.
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
If the points (3, -2), (x, 2), (8, 8) are collinear, then find the value of x.
If the points (2, -3), (k, -1), and (0, 4) are collinear, then find the value of 4k.
A(6, 1), B(8, 2) and C(9, 4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ∆ADE.
Find the cost of laying grass in a triangular field of sides 50 m, 65 m and 65 m at the rate of Rs 7 per m2.
In the given figure, ΔMNO is a right-angled triangle. Its legs are 6 cm and 8 cm long. Length of perpendicular NP on the side MO is ______.

