Advertisements
Advertisements
Question
How much paper of each shade is needed to make a kite given in the following figure, in which ABCD is a square with diagonal 44 cm.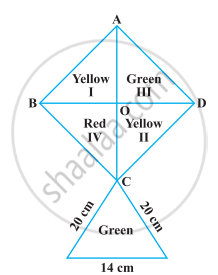
Solution
We know that, all the sides of a square are always equal.
i.e., AB = BC = CD = DA
In ΔACD, AC = 44 cm, ∠D = 90°
Using Pythagoras theorem in ΔACD,
AC2 = AD2 + DC2
⇒ 442 = AD2 + AD2 ...[∵ DC = AD]
⇒ 2AD2 = 44 × 44
⇒ AD2 = 22 × 44
⇒ AD = `sqrt(22 xx 44)` ...[Taking positive square root because length is always positive]
⇒ AD = `sqrt(2 xx 11 xx 4 xx 11)`
⇒ AD = `22sqrt(2)` cm
So, AB = BC = CD = DA = `22sqrt(2)` cm
∴ Area of square ABCD = Side × Side
= `22sqrt(2) xx 22sqrt(2)`
= 968 cm2
∴ Area of the red portion = `968/4` = 242 cm2 ...[Since, area of square is divided into four parts]
Now, area of the green portion = `968/4` = 242 cm2
Area of the yellow portion = `968/2` = 484 cm2
In ΔPCQ, side PC = a = 20 cm, CQ = b = 20 cm and PQ = c = 14 cm
`s = (a + b + c)/2`
= `(20 + 20 + 14)/2`
= `54/2`
= 27 cm
∴ Area of ΔPCQ = `sqrt(s(s - a)(s - b)(s - c))` ...[By Heron’s formula]
= `sqrt(27(27 - 20)(27 - 20)(27 - 14))`
= `sqrt(27 xx 7 xx 7 xx 13)`
= `sqrt(3 xx 3 xx 3 xx 7 xx 7 xx 13)`
= `21sqrt(39)`
= 21 × 6.24
= 131.04 cm2
∴ Total area of the green portion = (242 + 131.04) = 373.04 cm2
Hence, the paper required for each shade to make a kite is red paper 242 cm2, yellow paper 484 cm2 and green paper 373.04 cm2.
APPEARS IN
RELATED QUESTIONS
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Find the area of a quadrilateral ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm, DA =34 cm and diagonal BD =20 cm.
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
Find the area of a triangle formed by the lines 3x + y – 2 = 0, 5x + 2y – 3 = 0 and 2x – y – 3 = 0
Using Heron’s formula, find the area of a triangle whose sides are 10 cm, 24 cm, 26 cm
The perimeter of a triangular plot is 600 m. If the sides are in the ratio 5 : 12 : 13, then find the area of the plot
The perimeter of an equilateral triangle is 30 cm. The area is
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 13 m, 14 m and 15 m. The advertisements yield an earning of Rs 2000 per m2 a year. A company hired one of its walls for 6 months. How much rent did it pay?
A field is in the shape of a trapezium having parallel sides 90 m and 30 m. These sides meet the third side at right angles. The length of the fourth side is 100 m. If it costs Rs 4 to plough 1 m2 of the field, find the total cost of ploughing the field.
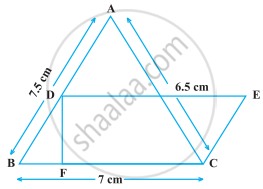
In the following figure, ∆ABC has sides AB = 7.5 cm, AC = 6.5 cm and BC = 7 cm. On base BC a parallelogram DBCE of same area as that of ∆ABC is constructed. Find the height DF of the parallelogram.