Advertisements
Advertisements
Question
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
Solution
Given that adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm.
Area of parallelogram = Area of ΔADC + area of ΔABC
[โต Diagonal of a parallelogram divides into two congruent triangles]
= 2 ×[๐ด๐๐๐ ๐๐ Δ๐ด๐ต๐ถ]
Now for Area of ΔABC
Let 2s = AB + BC + CA [โต Perimeter of ΔABC]
`⇒S=1/2(AB+BC+CA)`
`=S=1/2(34+20+42)`
`=1/2=(96)=48cm`
∴Area of ΔABC =`sqrt(s(s-ab))`
`=sqrt(48(48-34)(48-20)(48-42))`
`=sqrt(48(14)(28)(6))=336 cm^2`
∴๐ด๐๐๐ ๐๐ ๐๐๐๐๐๐๐๐๐๐๐๐๐ ๐ด๐ต๐ถ๐ท=2[๐ด๐๐๐ ๐๐ Δ๐ด๐ต๐ถ]=2×336=`672 cm^2`
APPEARS IN
RELATED QUESTIONS
The perimeter of a triangle is 300 m. If its sides are in the ratio 3 : 5 : 7. Find the area of the triangle ?
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
A rhombus sheet, whose perimeter is 32 m and whose one diagonal is 10 m long, is painted on both sides at the rate of Rs 5 per m2. Find the cost of painting.
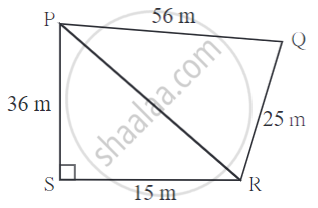
Look at the measures shown in the adjacent figure and find the area of โ PQRS.
If the points A(– 3, 9), B(a, b) and C(4, – 5) are collinear and if a + b = 1, then find a and b
The area of triangle formed by the points (− 5, 0), (0, – 5) and (5, 0) is
Using Heron’s formula, find the area of a triangle whose sides are 1.8 m, 8 m, 8.2 m
Find the area of the unshaded region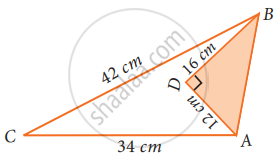
An isosceles right triangle has area 8 cm2. The length of its hypotenuse is ______.
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
