RD Sharma solutions for Mathematics [English] Class 9 chapter 17 - Heron’s Formula [Latest edition]

Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm ?

Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm ?

Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm ?

In a ΔABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ΔABC and hence its altitude on AC ?

The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle ?

The perimeter of a triangle is 300 m. If its sides are in the ratio 3 : 5 : 7. Find the area of the triangle ?

The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.

A triangle has sides 35 cm, 54 cm and 61 cm long. Find its area. Also, find the smallest of its altitudes ?

The lengths of the sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side.

The perimeter of an isosceles triangle is 42 cm and its baše is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.

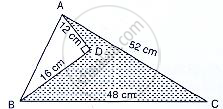
Find the area of the shaded region in the given figure.

Find the area of a quadrilateral ABCD is which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.

Area of PQRS = Area of PQR + Area of ΔPQS = (6+9.166)𝑐𝑚2=15.166𝑐𝑚2

The sides of a quadrilateral, taken in order are 5, 12, 14 and 15 meters respectively, and the angle contained by the first two sides is a right angle. Find its are

A park, in the shape of a quadrilateral ABCD, has ∠C = 900, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m How much area does it occupy?

Two parallel side of a trapezium are 60 cm and 77 cm and other sides are 25 cm and 26 cm. Find the area of the trapezium.

A rhombus sheet, whose perimeter is 32 m and whose one diagonal is 10 m long, is painted on both sides at the rate of Rs 5 per m2. Find the cost of painting.

Find the area of a quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90° and BCD forms an equilateral triangle whose each side is equal to 26 cm. (Take √3 = 1.73)

Find the area of a quadrilateral ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm, DA =34 cm and diagonal BD =20 cm.

The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.

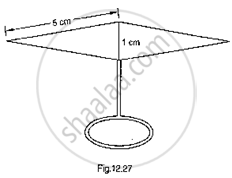
Find the area of the blades of thc magnetic compass shown in Fig.. 12.27. (Take √11 = 3.32).

A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 13 cm, 14 cm and 15 cm and the parallelogram stands on the base 14 cm, find the height of the parallelogram.

Find the area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m.

Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD =9 cm, CD = l2cm, ∠ACB = 90° and AC=l5cm.

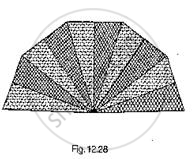
A hand fan is made by stitching lo equal size triangular strips of two different types of paper as shown in Fig. 12.28. The dimensions of equal strips are 25 cm, 25 cm and 14 cm. Find the area of each type of paper needed to make the hand fan.

The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.

Let Δ be the area of a triangle. Find the area of a triangle whose each side is twice the side of the given triangle.

If each side of a equilateral triangle is tripled then what is the percentage increase in the area of the triangle?

Mark the correct alternative in each of the following:
The sides of a triangle are 16 cm, 30 cm, 34 cm. Its area is

The base of an isosceles right triangle is 30 cm. Its area is

The sides of a triangle are 7 cm, 9 cm and 14 cm. Its area is

The sides of a triangular field are 325 m, 300 m and 125 m. Its area is

The sides of a triangle are 50 cm, 78 cm and 112 cm. The smallest altitude is

The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is

The sides of a triangle are 11 cm, 15 cm and 16 cm. The altitude to the largest side is

The base and hypotenuse of a right triangle are respectively 5 cm and 13 cm long. Its area is

If the area of an isosceles right triangle is 8 cm², what is the perimeter of the triangle?

The lengths of the sides of Δ ABC are consecutive integers. It Δ ABC has the same perimeter as an equilateral triangle with a side of length 9 cm, what is the length of the shortest side of ΔABC?

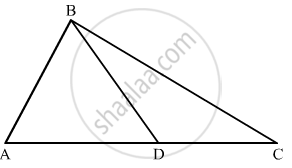
In the given figure, the ratio AD to DC is 3 to 2. If the area of Δ ABC is 40 cm², what is the area of Δ BDC?

If the length of a median of an equilateral triangle is x cm, then its area is

If every side of a triangle is doubled, then increase in the area of the triangle is

A square and an equilateral triangle have equal perimeters. If the diagonal of the square is \[12\sqrt{2}\]  cm, then area of the triangle is