Advertisements
Advertisements
Question
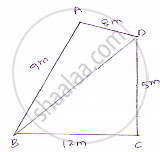
A park, in the shape of a quadrilateral ABCD, has ∠C = 900, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m How much area does it occupy?
Solution
Given sides of a quadrilaterals are AB = 9, BC = 12, CD = 05, DA = 08
Let us joint BD
In ΔBCD applying Pythagoras theorem.
`BD^2=BC^2+CD^2`
=`(12)^2+(5)^2`
=144+25
=169
𝐵𝐷=13𝑚
Area of ΔBCD = `1/2`×𝐵𝐶×𝐶𝐷=[`1/2`×12×5]`m^2=30m^2`
or ΔABD
`S=sqrt(perimeter)/2=sqrt(9+8+13)/2=15cm`
By heron’s formula`sqrt(s(s-a)(s-b)(s-c))`
Area of the triangle =`sqrt(15(15-9)(15-8)(15-13))m^2`
=`35.496 + 30 m^2`
= `65.5 m^2` (approximately)
APPEARS IN
RELATED QUESTIONS
A triangle and a parallelogram have the same base and the same area. If the sides of triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Find the area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m.
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD =9 cm, CD = l2cm, ∠ACB = 90° and AC=l5cm.
Let Δ be the area of a triangle. Find the area of a triangle whose each side is twice the side of the given triangle.
If each side of a triangle is doubled, the find percentage increase in its area.
Mark the correct alternative in each of the following:
The sides of a triangle are 16 cm, 30 cm, 34 cm. Its area is
Find the area of a quadrilateral ABCD whose sides are AB = 13 cm, BC = 12 cm, CD = 9 cm, AD = 14 cm and diagonal BD = 15 cm
The length of each side of an equilateral triangle having an area of `9sqrt(3)`cm2 is ______.
If the area of an equilateral triangle is `16sqrt(3)` cm2, then the perimeter of the triangle is ______.
The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is ______.
