Advertisements
Advertisements
Question
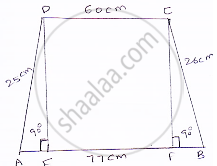
Two parallel side of a trapezium are 60 cm and 77 cm and other sides are 25 cm and 26 cm. Find the area of the trapezium.
Solution
Given that two parallel sides of trapezium are AB = 77 and CD = 60 cm
Other sides are BC = 26 m and AD = 25 cm.
Join AE and CF
Now, DE ⊥ AB and CF ⊥ AB
∴ DC = EF = 60 cm
Let AE = x
⇒ BF = 77 – 60 – x = 17 – x
`In ΔADE, DE^2 = AD^2 – AE^2 = 25^2 – x^2` [โต Pythagoras theorem]
And in ΔBCF, `CF^2= BC^2 – BF^2` [โต By Pythagoras theorem]
`⇒25=sqrt(26^2-(17-x)^2)`
`⇒25^2-x^2=25^2-(289-x^2-34-x)` [ โต`(a-b)^2=a^2-2ab+b^2` ]
`⇒265-x^2=676-289-x^2+34x`
`34x=238`
`x=7`
`∴ DE =sqrt(25^2-x^2)=sqrt(625-7^2)=sqrt(516)=24cm`
∴ Area of trapezium = `1/2`(๐ ๐ข๐ ๐๐ ๐๐๐๐๐๐๐๐ ๐ ๐๐๐๐ )×โ๐๐๐โ๐ก=`1/2`(60×77)×24=`1644cm^2`
APPEARS IN
RELATED QUESTIONS
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Area of PQRS = Area of PQR + Area of ΔPQS = (6+9.166)๐๐2=15.166๐๐2
A park, in the shape of a quadrilateral ABCD, has ∠C = 900, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m How much area does it occupy?
Find the area of an equilateral triangle having altitude h cm.
If each side of a triangle is doubled, the find percentage increase in its area.
The sides of a triangle are 7 cm, 9 cm and 14 cm. Its area is
The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is
The adjacent sides of a parallelogram measures 34 m, 20 m and the measure of the diagonal is 42 m. Find the area of parallelogram
The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is ______.
The area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm, is ______.
