Advertisements
Advertisements
Question
The adjacent sides of a parallelogram measures 34 m, 20 m and the measure of the diagonal is 42 m. Find the area of parallelogram
Solution
Since ABCD is a parallelogram opposite sides are equal.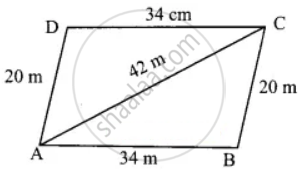
In the ΔABC
a = 20 m, b = 42 m and c = 34 m
s = `("a" + "b" + "c")/2`
= `(20 + 42 + 34)/2 "cm"`
= `96/2`
= 48 m
s – a = 48 – 20 = 28 m
s – b = 48 – 42 = 6 m
s – c = 48 – 34 = 14 m
Area of the ΔABC
= `sqrt("s"("s" - "a")("s" - "b")("s" - "c"))`
= `sqrt(48 xx 28 xx 6 xx 14)`
= `sqrt(2^4 xx 3 xx 2^2 xx 7 xx 2 xx 3 xx 2 xx 7)`
= `sqrt(2^8 xx 3^2 xx 7^2)`
= 24 × 3 × 7 sq.m
= 16 × 3 × 7 sq.m
= 336 sq.m
Since ABCD is a parallelogram
Area of ΔABC and Area of ΔACD are equal
Area of the parallelogram ABCD = (336 + 336) sq.m
= 672 sq.m
∴ Area of the parallelogram = 672 sq.m
APPEARS IN
RELATED QUESTIONS
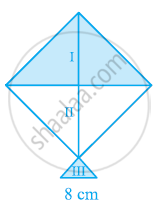
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangles of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it?
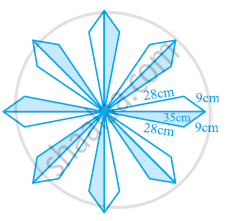
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50p per cm2.
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is
The perimeter of an equilateral triangle is 60 m. The area is ______.
The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude ______.
The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is ______.
The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
