Advertisements
Advertisements
Question
In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
Options
True
False
Solution
This statement is True.
Explanation:
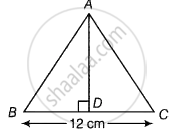
Since the sides of a triangle are a = 11 cm, b = 12 cm and c = 13 cm.
Now, semi-perimeter, `s = (a + b + c)/2`
= `(11 + 12 + 13)/2`
= `36/2`
= 18 cm
Area of a triangle = `sqrt(s(s - a)(s - b)(s - c))` ...[By Heron’s formula]
= `sqrt(18(18 - 11)(18 - 12)(18 - 13))`
= `sqrt(18 xx 7 xx 6 xx 5)`
= `sqrt(3 xx 6 xx 7 xx 6 xx 5)`
= `6sqrt(3 xx 7 xx 5)`
= `6sqrt(105)`
= 6 × 10.25
= 61.5 cm2
∴ Area of ΔABC = `1/2 xx BC xx AD` ...`[∵ "Area of triangle" = 1/2 ("base" xx "height")]`
= `1/2 xx 12 xx 10.25`
= 6 × 10.25
= 61.5 cm2
APPEARS IN
RELATED QUESTIONS
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Radha made a picture of an aeroplane with coloured papers as shown in the given figure. Find the total area of the paper used.
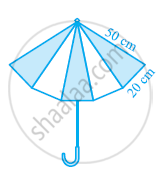
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see the given figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?
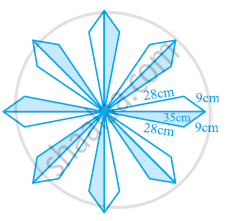
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50p per cm2.
Find the area of a quadrilateral ABCD is which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
The sides of a quadrilateral, taken in order are 5, 12, 14 and 15 meters respectively, and the angle contained by the first two sides is a right angle. Find its are
If each side of a equilateral triangle is tripled then what is the percentage increase in the area of the triangle?
Mark the correct alternative in each of the following:
The sides of a triangle are 16 cm, 30 cm, 34 cm. Its area is
The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is
A park is in the shape of a quadrilateral. The sides of the park are 15 m, 20 m, 26 m and 17 m and the angle between the first two sides is a right angle. Find the area of the park
