Advertisements
Advertisements
Question
Radha made a picture of an aeroplane with coloured papers as shown in the given figure. Find the total area of the paper used.
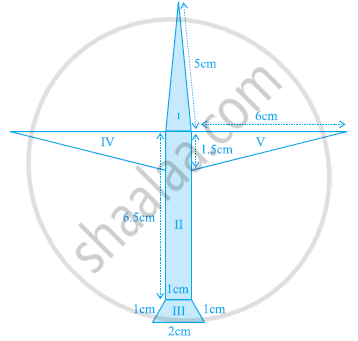
Solution
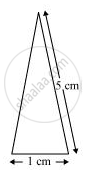
For triangle I
This triangle is an isosceles triangle.
Perimeter = 2s = (5 + 5 + 1) cm = 11cm
s = 11/2 = 5.5 cm
`"Area of triangle "=sqrt(s(s-a)(s-b)(s-c))`
`=[sqrt(5.5(5.5-5)(5.5-5)(5.5-1))]cm^2`
`=[sqrt((5.5)(0.5)(0.5)(4.5))]cm^2`
`=0.75sqrt11cm^2`
= (0.75 x 3.317) cm2
= 2.488 cm2 (Approximately)
For quadrilateral II
This quadrilateral is a rectangle.
Area = l × b = (6.5 × 1) cm2 = 6.5 cm2
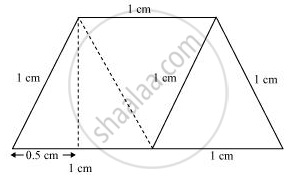
For quadrilateral III
This quadrilateral is a trapezium.
`"Perpendicular height of parallelogram "=(sqrt(1^2-(0.5)^2))cm = sqrt0.75 cm = 0.866 cm`
Area = Area of parallelogram + Area of equilateral triangle
`=(0.866)1+sqrt3/4(1)^2`
= 0.866 + 0.433
= 1.299 cm2
Area of triangle (IV) = Area of triangle in (V)
`=(1/2xx1.5xx6)cm^2`
= 4.5 cm2
Total area of the paper used = 2.488 + 6.5 + 1.299 + 4.5 × 2
= 19.287 cm2
APPEARS IN
RELATED QUESTIONS
Find the area of a quadrilateral ABCD is which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Find the area of an equilateral triangle having each side 4 cm.
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
If each side of a equilateral triangle is tripled then what is the percentage increase in the area of the triangle?
The base of an isosceles right triangle is 30 cm. Its area is
The sides of a triangle are 7 cm, 9 cm and 14 cm. Its area is
The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is
If the length of a median of an equilateral triangle is x cm, then its area is
Find the area of a quadrilateral ABCD whose sides are AB = 13 cm, BC = 12 cm, CD = 9 cm, AD = 14 cm and diagonal BD = 15 cm
In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
