Advertisements
Advertisements
Question
Find the area of a quadrilateral ABCD is which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Solution
For ΔPQR
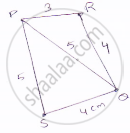
`PQ^2=QR^2+RP^2`
`(5^2)=(3)^2+(4)^2` [∵𝑃𝑅=3 𝑄𝑅=4 𝑎𝑛𝑑 𝑃𝑄=5]
So, ΔPQR is a right angled triangle. Right angle at point R.
Area of ΔABC =`1/2xxQRxxRP`
`=1/2xx3xx4`
`=6cm^2`
For ΔQPS
Perimeter = 2s = AC + CD + DA = (5 + 4 + 5)cm = 14 cm
S = 7 cm
By Heron’s formulae
Area of Δle`sqrt(s(s-a)(s-b)(s-c))cm^2`
Area of Δle PQS `=sqrt(7(7-5)(7-4)(7-3))cm^2`
`=2sqrt(21)cm^2`
`=(2xx4.583)cm^2`
`=9.166cm^2`
Area of PQRS = Area of PQR + Area of ΔPQS = `(6+9.166)cm^2=15.166 cm^2`
APPEARS IN
RELATED QUESTIONS
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
A triangle and a parallelogram have the same base and the same area. If the sides of triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
The sides of a quadrilateral, taken in order are 5, 12, 14 and 15 meters respectively, and the angle contained by the first two sides is a right angle. Find its are
Find the area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m.
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD =9 cm, CD = l2cm, ∠ACB = 90° and AC=l5cm.
The lengths of the sides of Δ ABC are consecutive integers. It Δ ABC has the same perimeter as an equilateral triangle with a side of length 9 cm, what is the length of the shortest side of ΔABC?
If every side of a triangle is doubled, then increase in the area of the triangle is
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is \[12\sqrt{2}\] cm, then area of the triangle is
The area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm, is ______.
The area of the equilateral triangle is `20sqrt(3)` cm2 whose each side is 8 cm.
