Advertisements
Advertisements
Questions
Area of PQRS = Area of PQR + Area of ΔPQS = (6+9.166)𝑐𝑚2=15.166𝑐𝑚2
The sides of a quadrangular field, taken in order are 26 m, 27 m, 7 m are 24 m respectively. The angle contained by the last two sides is a right angle. Find its area.
Solution
The sides of a quadrilateral field taken order as AB = 26m
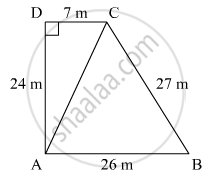
BC = 27 m
CD = 7m and DA = 24 m
Diagonal AC is joined
Now ΔADC
By applying Pythagoras theorem
⇒`AC^2=AD^2+CD^2`
⇒`AC=sqrt(AD^2 +CD^2)`
⇒`AC=sqrt(24^2+7^2)`
⇒`AC=sqrt625=25 m`
Now area of ΔABC
`S=1/2(AB+BC+CA)=1/2(26+27+25)=78/2=39 m`
By using heron’s formula
Area (ΔABC) = `sqrt(S(S-AD)(S_BC)(S-CA))`
`=sqrt(39(39-26)(39-21)(39-25))`
`sqrt(39xx14xx13xx12xx1)`
`=291.849cm^2`
Now for area of ΔADC
`S=1/2(AD+CD+AC)`
`=1/2(25+24+7)=28cm`
By using heron’s formula
`∴ Area of ΔADC = sqrt(S(S-AD)(S-DC)(S-CA))`
`=sqrt(28(28-24)(28-7)(28-25))`
`=84m^2`
∴ Area of rectangular field ABCD = area of ΔABC + area of ΔADC
= `291.849+84`
= `375.8m^2`
APPEARS IN
RELATED QUESTIONS
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
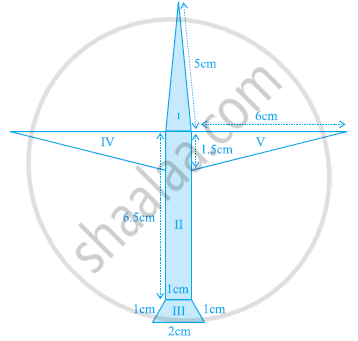
Radha made a picture of an aeroplane with coloured papers as shown in the given figure. Find the total area of the paper used.
Find the area of an equilateral triangle having each side 4 cm.
Find the area of an equilateral triangle having each side x cm.
Mark the correct alternative in each of the following:
The sides of a triangle are 16 cm, 30 cm, 34 cm. Its area is
The sides of a triangular field are 325 m, 300 m and 125 m. Its area is
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is \[12\sqrt{2}\] cm, then area of the triangle is
A land is in the shape of rhombus. The perimeter of the land is 160 m and one of the diagonal is 48 m. Find the area of the land.
The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is ______.
