Advertisements
Advertisements
Question
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is \[12\sqrt{2}\] cm, then area of the triangle is
Options
- \[24\sqrt{2} c m^2\]
- \[24\sqrt{3} c m^2\]
- \[48\sqrt{3} c m^2\]
- \[64\sqrt{3} c m^2\]
Solution
It is given the perimeter of a square ABCD is equal to the perimeter of triangle PQR.
The measure of the diagonal of the square is given `12 sqrt(2)` cm.We are asked to find the area of the triangle
In square ABCD, we assume that the adjacent sides of square be a.
Since, it is a square then a= b
By using Pythagorean Theorem
`a^2 +b^2 = (12sqrt(2))^2`
`a^2 +a^2 = 288`
`2a^2 = 288`
`a^2 = 288/2`
` a = sqrt(144)`
a = 12 cm
Therefore, side of the square is 12 cm.
Perimeter of the square ABCD say P is given by
p = 4 × side
Side = 12 cm
p = 4 × 12
p = 48 cm
Perimeter of the equilateral triangle PQR say P1 is given by
p1= 3 × side
p = p1
p = 3 × side
48 = 3 × side
side = `48/3`
side = 16 cm
The side of equilateral triangle PQR is equal to 16 cm.
Area of an equilateral triangle say A, having each side a cm is given by
`A = sqrt(3)/4 a^2`
Area of the given equilateral triangle having each equal side equal to 4 cm is given by
a = 16 cm
`A = sqrt(3)/4 (16)^2 `
`A = sqrt(3)/4 xx 256`
`A=64 sqrt(3) cm^2`
APPEARS IN
RELATED QUESTIONS
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
A triangle and a parallelogram have the same base and the same area. If the sides of triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
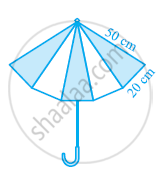
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see the given figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?
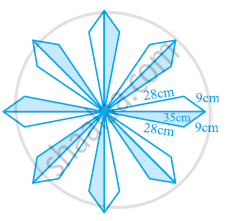
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50p per cm2.
Area of PQRS = Area of PQR + Area of ΔPQS = (6+9.166)𝑐𝑚2=15.166𝑐𝑚2
Find the area of an equilateral triangle having each side x cm.
Find the area of an equilateral triangle having altitude h cm.
The sides of a triangular field are 325 m, 300 m and 125 m. Its area is
The perimeter of an equilateral triangle is 60 m. The area is ______.
The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
