Advertisements
Advertisements
प्रश्न
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is \[12\sqrt{2}\] cm, then area of the triangle is
विकल्प
- \[24\sqrt{2} c m^2\]
- \[24\sqrt{3} c m^2\]
- \[48\sqrt{3} c m^2\]
- \[64\sqrt{3} c m^2\]
उत्तर
It is given the perimeter of a square ABCD is equal to the perimeter of triangle PQR.
The measure of the diagonal of the square is given `12 sqrt(2)` cm.We are asked to find the area of the triangle
In square ABCD, we assume that the adjacent sides of square be a.
Since, it is a square then a= b
By using Pythagorean Theorem
`a^2 +b^2 = (12sqrt(2))^2`
`a^2 +a^2 = 288`
`2a^2 = 288`
`a^2 = 288/2`
` a = sqrt(144)`
a = 12 cm
Therefore, side of the square is 12 cm.
Perimeter of the square ABCD say P is given by
p = 4 × side
Side = 12 cm
p = 4 × 12
p = 48 cm
Perimeter of the equilateral triangle PQR say P1 is given by
p1= 3 × side
p = p1
p = 3 × side
48 = 3 × side
side = `48/3`
side = 16 cm
The side of equilateral triangle PQR is equal to 16 cm.
Area of an equilateral triangle say A, having each side a cm is given by
`A = sqrt(3)/4 a^2`
Area of the given equilateral triangle having each equal side equal to 4 cm is given by
a = 16 cm
`A = sqrt(3)/4 (16)^2 `
`A = sqrt(3)/4 xx 256`
`A=64 sqrt(3) cm^2`
APPEARS IN
संबंधित प्रश्न
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
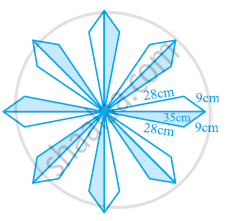
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50p per cm2.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
The base of an isosceles right triangle is 30 cm. Its area is
The sides of a triangle are 50 cm, 78 cm and 112 cm. The smallest altitude is
The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is
If the area of an isosceles right triangle is 8 cm2, what is the perimeter of the triangle?
The length of each side of an equilateral triangle having an area of `9sqrt(3)`cm2 is ______.
The area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm, is ______.
The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is ______.
