Advertisements
Advertisements
प्रश्न
If every side of a triangle is doubled, then increase in the area of the triangle is
विकल्प
- \[100\sqrt{2} \] %
200%
300%
400%
उत्तर
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
`A = sqrt(s(s-a)(s-b)(s-c))`, where
`s = (a+b+c)/2 ⇒ 2s = a + b + c`
We take the sides of a new triangle as 2a, 2b, 2c that is twice the sides of previous one
Now, the area of a triangle having sides 2a, 2b, and 2c and s1 as semi-perimeter is given by,
`A_1 = sqrt(s_1(s_1-2a)(s_1 - 2b)(s_1 - 2c) `
Where,
`s_1 = (2a +2b+2c)/2`
`s_1 = (2(a+b+c))/2`
s1 = a + b + c
s1 = 2s
Now,
`A_1 = sqrt(2s (2s-2a)(2s-2b)(2s-2c))`
`A
_1 = sqrt(2s xx 2 ( s-a)xx 2 ( s-b) xx 2 (s-c))`
`A_1 = 4 sqrt(s (s-a)(s-b)(s-c))`
`A_1 = 4A`
Therefore, increase in the area of the triangle
=A1 - A
=4A - A
=3 A Percentage increase in area
`= (3A)/A xx 100`
= 300 %
APPEARS IN
संबंधित प्रश्न
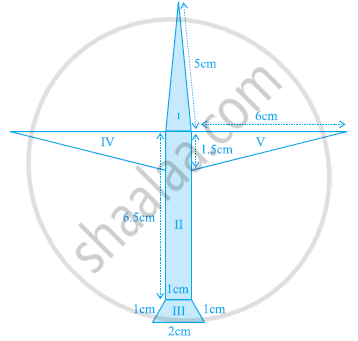
Radha made a picture of an aeroplane with coloured papers as shown in the given figure. Find the total area of the paper used.
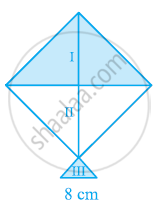
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangles of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it?
Find the area of a quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90° and BCD forms an equilateral triangle whose each side is equal to 26 cm. (Take √3 = 1.73)
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD =9 cm, CD = l2cm, ∠ACB = 90° and AC=l5cm.
If each side of a triangle is doubled, the find percentage increase in its area.
The base of an isosceles right triangle is 30 cm. Its area is
The perimeter of an equilateral triangle is 60 m. The area is ______.
The area of the equilateral triangle is `20sqrt(3)` cm2 whose each side is 8 cm.
The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
