Advertisements
Advertisements
प्रश्न
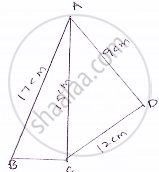
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD =9 cm, CD = l2cm, ∠ACB = 90° and AC=l5cm.
उत्तर
The sides of a quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB = 90° and AC = 15 cm
Here, By using Pythagoras theorem
`BC=sqrt(17^2-15^2) = sqrt(289-225)=sqrt64=8cm`
Now, area of ΔABC=`1/2xx8xx15=60cm^2`
For area of Δle ACD,
Let a = 15 cm, b = 12 cm and c = 9 cm
Therefore, S =`(15+12+9)/2=36/2=18cm`
Area of ACD =`sqrt(s(s-a)(s-b)(s-c))`
`=sqrt(18(18-15)(18-12)(18-9))`
`=sqrt(18xx18xx3xx3)`
`=sqrt((18xx3)^2)`
`=54cm^2`
∴ Thus, the area of quadrilateral ABCD = `60 + 54 = 114 cm^2`
APPEARS IN
संबंधित प्रश्न
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
A triangle and a parallelogram have the same base and the same area. If the sides of triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Find the area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m.
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
Let Δ be the area of a triangle. Find the area of a triangle whose each side is twice the side of the given triangle.
A park is in the shape of a quadrilateral. The sides of the park are 15 m, 20 m, 26 m and 17 m and the angle between the first two sides is a right angle. Find the area of the park
The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is ______.
The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is ______.
The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
