Advertisements
Advertisements
प्रश्न
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Advertisements
उत्तर
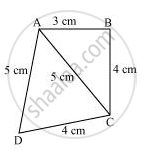
For ΔABC,
AC2 = AB2 + BC2
(5)2 = (3)2 + (4)2
Therefore, ΔABC is a right-angled triangle, right-angled at point B.
Area of ΔABC`= 1/2xxABxxBC=1/2xx3xx4=6 cm^2`
For ΔADC,
Perimeter = 2s = AC + CD + DA = (5 + 4 + 5) cm = 14 cm
s = 14/2 = 7 cm
By Heron’s formula,
`"Area of triangle "=sqrt(s(s-a)(s-b)(s-c))`
`"Area of "triangle ADC=[sqrt(7(7-5)(7-5)(7-4))]cm^2`
`=(sqrt(7xx2xx2xx3))cm^2`
`=2sqrt21 cm^2`
= (2 x 4.583) cm2
= 9.166 cm2
Area of ABCD = Area of ΔABC + Area of ΔACD
= (6 + 9.166) cm2
= 15.166 cm2
= 15.2 cm2 (approximately)
संबंधित प्रश्न
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see the given figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?
The sides of a quadrilateral, taken in order are 5, 12, 14 and 15 meters respectively, and the angle contained by the first two sides is a right angle. Find its are
Two parallel side of a trapezium are 60 cm and 77 cm and other sides are 25 cm and 26 cm. Find the area of the trapezium.
Find the area of a quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90° and BCD forms an equilateral triangle whose each side is equal to 26 cm. (Take √3 = 1.73)
Find the area of an equilateral triangle having altitude h cm.
If each side of a triangle is doubled, the find percentage increase in its area.
Mark the correct alternative in each of the following:
The sides of a triangle are 16 cm, 30 cm, 34 cm. Its area is
Find the area of a quadrilateral ABCD whose sides are AB = 13 cm, BC = 12 cm, CD = 9 cm, AD = 14 cm and diagonal BD = 15 cm
A park is in the shape of a quadrilateral. The sides of the park are 15 m, 20 m, 26 m and 17 m and the angle between the first two sides is a right angle. Find the area of the park
