Advertisements
Advertisements
प्रश्न
The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude ______.
विकल्प
`16sqrt(5)` cm
`10sqrt(5)` cm
`24sqrt(5)` cm
28 cm
उत्तर
The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude `underlinebb(24sqrt(5) cm)`.
Explanation:
Given: The sides of a triangle area = 35 cm, b = 54 cm and c = 61 cm, respectively.
So, semi-perimeter of a triangle is:
`s = (a + b + c)/2`
= `(35 + 54 + 61)/2`
= `150/2`
= 75
Area of triangle = `sqrt(s(s - a)(s - b)(s - c))`
= `sqrt(75(75 - 35)(75 - 54)(75 - 61))`
= `sqrt(75 xx 40 xx 21 xx 14)`
= `sqrt(5 xx 5 xx 3 xx 2 xx 2 xx 2 xx 5 xx 3 xx 7 xx 7 xx 2)`
= `5 xx 3 xx 2 xx 2 xx 7sqrt(5)`
= `420sqrt(5)`
As know that,
Area of triangle ABC = `1/2` × Base × Altitude
`1/2` × 35 × Altitude = `420sqrt(5)`
Altitude = `(420sqrt(5) xx 2)/35`
Altitude = `24sqrt(5)`
Therefore, the length of altitude is `24sqrt(5)`.
APPEARS IN
संबंधित प्रश्न
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangles of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it?
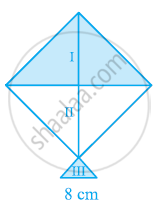
Area of PQRS = Area of PQR + Area of ΔPQS = (6+9.166)𝑐𝑚2=15.166𝑐𝑚2
A park, in the shape of a quadrilateral ABCD, has ∠C = 900, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m How much area does it occupy?
Let Δ be the area of a triangle. Find the area of a triangle whose each side is twice the side of the given triangle.
If each side of a equilateral triangle is tripled then what is the percentage increase in the area of the triangle?
The base and hypotenuse of a right triangle are respectively 5 cm and 13 cm long. Its area is
The lengths of the sides of Δ ABC are consecutive integers. It Δ ABC has the same perimeter as an equilateral triangle with a side of length 9 cm, what is the length of the shortest side of ΔABC?
A land is in the shape of rhombus. The perimeter of the land is 160 m and one of the diagonal is 48 m. Find the area of the land.
The adjacent sides of a parallelogram measures 34 m, 20 m and the measure of the diagonal is 42 m. Find the area of parallelogram
The area of an equilateral triangle with side `2sqrt(3)` cm is ______.
