Advertisements
Advertisements
प्रश्न
The area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm, is ______.
विकल्प
`sqrt(15)` cm2
`sqrt(15/2)` cm2
`2sqrt(15)` cm2
`4sqrt(15)` cm2
उत्तर
The area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm, is `underlinebb(sqrt(15) cm^2)`.
Explanation:
a = 2, b = 4, c = 4
`s = (a + b + c)/2`
⇒ `s = (2 + 4 + 4)/2 = 10/2 = 5`
Area (Δ) = `sqrt(s(s - a)(s - b)(s - c))`
⇒ Area (Δ) = `sqrt(5(5 - 2)(5 - 4)(5 - 4))`
⇒ Area (Δ) = `sqrt(5 xx 3 xx 1 xx 1`
⇒ Area (Δ) = `sqrt(15)` cm2
APPEARS IN
संबंधित प्रश्न
Two parallel side of a trapezium are 60 cm and 77 cm and other sides are 25 cm and 26 cm. Find the area of the trapezium.
Find the area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m.
The sides of a triangle are 7 cm, 9 cm and 14 cm. Its area is
The lengths of the sides of Δ ABC are consecutive integers. It Δ ABC has the same perimeter as an equilateral triangle with a side of length 9 cm, what is the length of the shortest side of ΔABC?
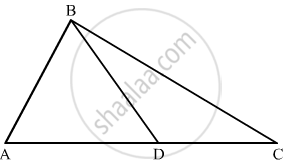
In the given figure, the ratio AD to DC is 3 to 2. If the area of Δ ABC is 40 cm2, what is the area of Δ BDC?
If the length of a median of an equilateral triangle is x cm, then its area is
Find the area of a quadrilateral ABCD whose sides are AB = 13 cm, BC = 12 cm, CD = 9 cm, AD = 14 cm and diagonal BD = 15 cm
A land is in the shape of rhombus. The perimeter of the land is 160 m and one of the diagonal is 48 m. Find the area of the land.
The area of the equilateral triangle is `20sqrt(3)` cm2 whose each side is 8 cm.
The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
