Advertisements
Advertisements
प्रश्न
If the length of a median of an equilateral triangle is x cm, then its area is
विकल्प
x2
- \[\frac{\sqrt{3}}{2} x^2\]
- \[\frac{x^2}{\sqrt{3}}\]
- \[\frac{x^2}{2}\]
उत्तर
We are given the length of median of an equilateral triangle by which we can calculate its side. We are asked to find area of triangle in terms of x
Altitude of an equilateral triangle say L, having equal sides of a cm is given by, where, L = x cm
`x = sqrt(3)/2 a`
`a = 2/sqrt(3) x cm `
Area of an equilateral triangle, say A1 having each side a cm is given by
`A_1 = sqrt(3)/4 a^2`
Since `a = 2/sqrt(3) x cm `.So
`A_1 = sqrt (3)/4 (2/sqrt(3) x )^2`
`A_1 = sqrt(3)/4 xx (4x^2)/3`
`A_1 = x^2/sqrt(3)`
APPEARS IN
संबंधित प्रश्न
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
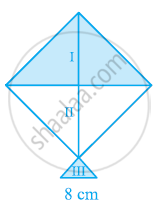
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangles of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it?
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Find the area of a quadrilateral ABCD is which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
If each side of a equilateral triangle is tripled then what is the percentage increase in the area of the triangle?
The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is
The base and hypotenuse of a right triangle are respectively 5 cm and 13 cm long. Its area is
Find the area of a quadrilateral ABCD whose sides are AB = 13 cm, BC = 12 cm, CD = 9 cm, AD = 14 cm and diagonal BD = 15 cm
The length of each side of an equilateral triangle having an area of `9sqrt(3)`cm2 is ______.
In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
