Advertisements
Advertisements
प्रश्न
If the length of a median of an equilateral triangle is x cm, then its area is
पर्याय
x2
- \[\frac{\sqrt{3}}{2} x^2\]
- \[\frac{x^2}{\sqrt{3}}\]
- \[\frac{x^2}{2}\]
उत्तर
We are given the length of median of an equilateral triangle by which we can calculate its side. We are asked to find area of triangle in terms of x
Altitude of an equilateral triangle say L, having equal sides of a cm is given by, where, L = x cm
`x = sqrt(3)/2 a`
`a = 2/sqrt(3) x cm `
Area of an equilateral triangle, say A1 having each side a cm is given by
`A_1 = sqrt(3)/4 a^2`
Since `a = 2/sqrt(3) x cm `.So
`A_1 = sqrt (3)/4 (2/sqrt(3) x )^2`
`A_1 = sqrt(3)/4 xx (4x^2)/3`
`A_1 = x^2/sqrt(3)`
APPEARS IN
संबंधित प्रश्न
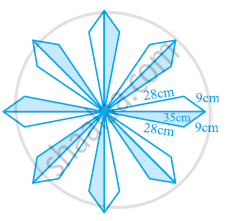
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50p per cm2.
Find the area of an equilateral triangle having each side 4 cm.
Find the area of an equilateral triangle having altitude h cm.
The base of an isosceles right triangle is 30 cm. Its area is
The sides of a triangle are 50 cm, 78 cm and 112 cm. The smallest altitude is
The base and hypotenuse of a right triangle are respectively 5 cm and 13 cm long. Its area is
If the area of an isosceles right triangle is 8 cm2, what is the perimeter of the triangle?
The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is ______.
The area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm, is ______.
The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is ______.
