Advertisements
Advertisements
प्रश्न
If the area of an isosceles right triangle is 8 cm2, what is the perimeter of the triangle?
पर्याय
8 + \[\sqrt{2}\] cm2
8 + 4 \[\sqrt{2}\] cm2
4+ 8 \[\sqrt{2}\] cm2
12 \[\sqrt{2}\] cm2
उत्तर
We are given the area of an isosceles right triangle and we have to find its perimeter.
Two sides of isosceles right triangle are equal and we assume the equal sides to be the base and height of the triangle. We are asked to find the perimeter of the triangle
Let us take the base and height of the triangle be x cm.
Area of a isosceles right triangle, say A having base x cm and
height x cm is given by `A = 1/2 (" Base" xx "Height " )`
A = 8 cm2; Base = Height = x cm
`8=1/2 (x xx x)`
8 × 2 = (x)2
x = `sqrt(16)`
x = 4 cm
Using Pythagorean Theorem we have;
(Hypotenuse )2 = ( Base)2 + (Height )2
(Hypotenuse )2 = (4)2 + (4)2
(Hypotenuse )2 = 16 + 16
Hypotenuse = `sqrt(32)`
Hypotenuse = 4` sqrt(2)` cm
Let ABC be the given triangle
Perimeter of triangle ABC, say P is given by
p = AB + BC + AC
AB = 4 cm; BC = 4 cm; AC = `4 sqrt(2)`
`p = 4 + 4 + 4 sqrt(2)`
`p = 8 + 4 sqrt(2) ` cm
APPEARS IN
संबंधित प्रश्न
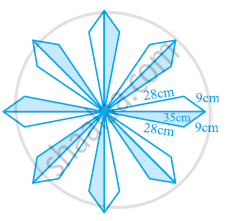
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50p per cm2.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Area of PQRS = Area of PQR + Area of ΔPQS = (6+9.166)𝑐𝑚2=15.166𝑐𝑚2
The base of an isosceles right triangle is 30 cm. Its area is
The sides of a triangle are 7 cm, 9 cm and 14 cm. Its area is
The lengths of the sides of Δ ABC are consecutive integers. It Δ ABC has the same perimeter as an equilateral triangle with a side of length 9 cm, what is the length of the shortest side of ΔABC?
If the length of a median of an equilateral triangle is x cm, then its area is
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is \[12\sqrt{2}\] cm, then area of the triangle is
The area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm, is ______.
