Advertisements
Advertisements
प्रश्न
If the area of an isosceles right triangle is 8 cm2, what is the perimeter of the triangle?
विकल्प
8 + \[\sqrt{2}\] cm2
8 + 4 \[\sqrt{2}\] cm2
4+ 8 \[\sqrt{2}\] cm2
12 \[\sqrt{2}\] cm2
उत्तर
We are given the area of an isosceles right triangle and we have to find its perimeter.
Two sides of isosceles right triangle are equal and we assume the equal sides to be the base and height of the triangle. We are asked to find the perimeter of the triangle
Let us take the base and height of the triangle be x cm.
Area of a isosceles right triangle, say A having base x cm and
height x cm is given by `A = 1/2 (" Base" xx "Height " )`
A = 8 cm2; Base = Height = x cm
`8=1/2 (x xx x)`
8 × 2 = (x)2
x = `sqrt(16)`
x = 4 cm
Using Pythagorean Theorem we have;
(Hypotenuse )2 = ( Base)2 + (Height )2
(Hypotenuse )2 = (4)2 + (4)2
(Hypotenuse )2 = 16 + 16
Hypotenuse = `sqrt(32)`
Hypotenuse = 4` sqrt(2)` cm
Let ABC be the given triangle
Perimeter of triangle ABC, say P is given by
p = AB + BC + AC
AB = 4 cm; BC = 4 cm; AC = `4 sqrt(2)`
`p = 4 + 4 + 4 sqrt(2)`
`p = 8 + 4 sqrt(2) ` cm
APPEARS IN
संबंधित प्रश्न
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Find the area of an equilateral triangle having each side x cm.
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is
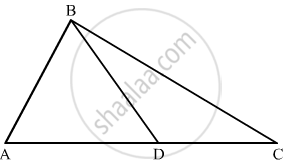
In the given figure, the ratio AD to DC is 3 to 2. If the area of Δ ABC is 40 cm2, what is the area of Δ BDC?
The length of each side of an equilateral triangle having an area of `9sqrt(3)`cm2 is ______.
The area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm, is ______.
The area of the equilateral triangle is `20sqrt(3)` cm2 whose each side is 8 cm.
The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
