Advertisements
Advertisements
प्रश्न
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
उत्तर
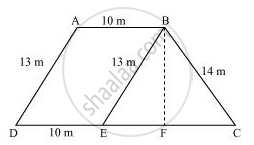
Draw a line BE parallel to AD and draw a perpendicular BF on CD.
It can be observed that ABED is a parallelogram.
BE = AD = 13 m
ED = AB = 10 m
EC = 25 − ED = 15 m
For ΔBEC,
Semi-perimeter,
`s=(13+14+15)/2=21 m`
By Heron’s formula,
`"Area of triangle "=sqrt(s(s-a)(s-b)(s-c))`
`"Area of ΔBEC "=[sqrt(21(21-13)(21-14)(21-15))]m^2`
`=[sqrt(21(8)(7)(6))]m^2`
= 84 m2
`"Area of ΔBEC "=1/2xxCExxBF`
`rArr84=1/2xx15xxBF`
`rArrBF=168/15=11.2 m`
Area of ABED = BF × DE = 11.2 × 10 = 112 m2
Area of the field = 84 + 112 = 196 m2
APPEARS IN
संबंधित प्रश्न
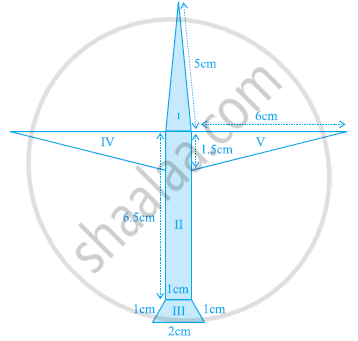
Radha made a picture of an aeroplane with coloured papers as shown in the given figure. Find the total area of the paper used.
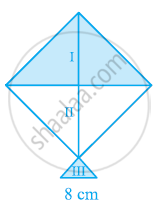
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangles of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it?
Find the area of a quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90° and BCD forms an equilateral triangle whose each side is equal to 26 cm. (Take √3 = 1.73)
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
Find the area of an equilateral triangle having altitude h cm.
Let Δ be the area of a triangle. Find the area of a triangle whose each side is twice the side of the given triangle.
The base of an isosceles right triangle is 30 cm. Its area is
The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is
The area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm, is ______.
In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
