Advertisements
Advertisements
प्रश्न
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is \[12\sqrt{2}\] cm, then area of the triangle is
पर्याय
- \[24\sqrt{2} c m^2\]
- \[24\sqrt{3} c m^2\]
- \[48\sqrt{3} c m^2\]
- \[64\sqrt{3} c m^2\]
उत्तर
It is given the perimeter of a square ABCD is equal to the perimeter of triangle PQR.
The measure of the diagonal of the square is given `12 sqrt(2)` cm.We are asked to find the area of the triangle
In square ABCD, we assume that the adjacent sides of square be a.
Since, it is a square then a= b
By using Pythagorean Theorem
`a^2 +b^2 = (12sqrt(2))^2`
`a^2 +a^2 = 288`
`2a^2 = 288`
`a^2 = 288/2`
` a = sqrt(144)`
a = 12 cm
Therefore, side of the square is 12 cm.
Perimeter of the square ABCD say P is given by
p = 4 × side
Side = 12 cm
p = 4 × 12
p = 48 cm
Perimeter of the equilateral triangle PQR say P1 is given by
p1= 3 × side
p = p1
p = 3 × side
48 = 3 × side
side = `48/3`
side = 16 cm
The side of equilateral triangle PQR is equal to 16 cm.
Area of an equilateral triangle say A, having each side a cm is given by
`A = sqrt(3)/4 a^2`
Area of the given equilateral triangle having each equal side equal to 4 cm is given by
a = 16 cm
`A = sqrt(3)/4 (16)^2 `
`A = sqrt(3)/4 xx 256`
`A=64 sqrt(3) cm^2`
APPEARS IN
संबंधित प्रश्न
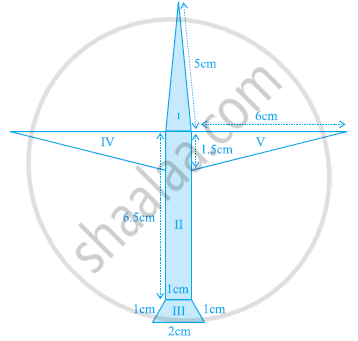
Radha made a picture of an aeroplane with coloured papers as shown in the given figure. Find the total area of the paper used.
A triangle and a parallelogram have the same base and the same area. If the sides of triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Find the area of a quadrilateral ABCD is which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Find the area of an equilateral triangle having each side 4 cm.
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
Mark the correct alternative in each of the following:
The sides of a triangle are 16 cm, 30 cm, 34 cm. Its area is
The base of an isosceles right triangle is 30 cm. Its area is
The sides of a triangle are 11 cm, 15 cm and 16 cm. The altitude to the largest side is
A land is in the shape of rhombus. The perimeter of the land is 160 m and one of the diagonal is 48 m. Find the area of the land.
In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
