Advertisements
Advertisements
प्रश्न
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
उत्तर
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
`A = sqrt(s(s-a)(s-b)(s-c))`, where,
`s = (a+b+c)/2`
It is given the sides of a triangular field are in the ratio 3:4:5 and perimeter=144 m
Therefore, a: b: c = 3:4:5
We will assume the sides of triangular field as
a= 3x : b = 4x ; c = 5x
2s = 144
`s= 144/2`
s= 72
`72= (3x+4x+5x)/2`
72×2= 12x
` x = 144/12`
x = 12
Substituting the value of x in, we get sides of the triangle as
a = 3x = 3 × 12
a = 36 m
b = 4x = 4 × 12
b = 48 m
c = 5x = 5 × 12
c = 60 m
Area of a triangular field, say A having sides a, b , c and s as semi-perimeter is given by
a = 36 m ; b = 48 m ; c = 60 m
s = 72 m
`A = sqrt( 72(72-36) (72-48)(72-60)`
`A=sqrt(72(36)(24)(12))`
`A= sqrt(746496)`
A = 864 m2
APPEARS IN
संबंधित प्रश्न
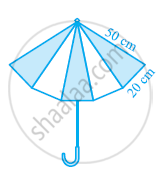
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see the given figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Two parallel side of a trapezium are 60 cm and 77 cm and other sides are 25 cm and 26 cm. Find the area of the trapezium.
Find the area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m.
Find the area of an equilateral triangle having altitude h cm.
If each side of a triangle is doubled, the find percentage increase in its area.
The sides of a triangular field are 325 m, 300 m and 125 m. Its area is
The sides of a triangle are 11 cm, 15 cm and 16 cm. The altitude to the largest side is
If the length of a median of an equilateral triangle is x cm, then its area is
The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude ______.
