Advertisements
Advertisements
प्रश्न
The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude ______.
पर्याय
`16sqrt(5)` cm
`10sqrt(5)` cm
`24sqrt(5)` cm
28 cm
उत्तर
The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude `underlinebb(24sqrt(5) cm)`.
Explanation:
Given: The sides of a triangle area = 35 cm, b = 54 cm and c = 61 cm, respectively.
So, semi-perimeter of a triangle is:
`s = (a + b + c)/2`
= `(35 + 54 + 61)/2`
= `150/2`
= 75
Area of triangle = `sqrt(s(s - a)(s - b)(s - c))`
= `sqrt(75(75 - 35)(75 - 54)(75 - 61))`
= `sqrt(75 xx 40 xx 21 xx 14)`
= `sqrt(5 xx 5 xx 3 xx 2 xx 2 xx 2 xx 5 xx 3 xx 7 xx 7 xx 2)`
= `5 xx 3 xx 2 xx 2 xx 7sqrt(5)`
= `420sqrt(5)`
As know that,
Area of triangle ABC = `1/2` × Base × Altitude
`1/2` × 35 × Altitude = `420sqrt(5)`
Altitude = `(420sqrt(5) xx 2)/35`
Altitude = `24sqrt(5)`
Therefore, the length of altitude is `24sqrt(5)`.
APPEARS IN
संबंधित प्रश्न
Radha made a picture of an aeroplane with coloured papers as shown in the given figure. Find the total area of the paper used.
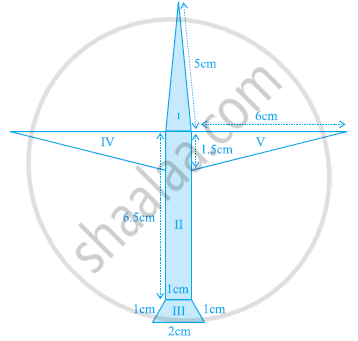
Find the area of a quadrilateral ABCD is which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
The sides of a quadrilateral, taken in order are 5, 12, 14 and 15 meters respectively, and the angle contained by the first two sides is a right angle. Find its are
Two parallel side of a trapezium are 60 cm and 77 cm and other sides are 25 cm and 26 cm. Find the area of the trapezium.
Find the area of an equilateral triangle having each side x cm.
The sides of a triangle are 7 cm, 9 cm and 14 cm. Its area is
The adjacent sides of a parallelogram measures 34 m, 20 m and the measure of the diagonal is 42 m. Find the area of parallelogram
The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is ______.
The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is ______.
In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
