Advertisements
Advertisements
प्रश्न
In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
पर्याय
True
False
Advertisements
उत्तर
This statement is True.
Explanation:
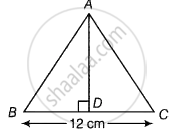
Since the sides of a triangle are a = 11 cm, b = 12 cm and c = 13 cm.
Now, semi-perimeter, `s = (a + b + c)/2`
= `(11 + 12 + 13)/2`
= `36/2`
= 18 cm
Area of a triangle = `sqrt(s(s - a)(s - b)(s - c))` ...[By Heron’s formula]
= `sqrt(18(18 - 11)(18 - 12)(18 - 13))`
= `sqrt(18 xx 7 xx 6 xx 5)`
= `sqrt(3 xx 6 xx 7 xx 6 xx 5)`
= `6sqrt(3 xx 7 xx 5)`
= `6sqrt(105)`
= 6 × 10.25
= 61.5 cm2
∴ Area of ΔABC = `1/2 xx BC xx AD` ...`[∵ "Area of triangle" = 1/2 ("base" xx "height")]`
= `1/2 xx 12 xx 10.25`
= 6 × 10.25
= 61.5 cm2
APPEARS IN
संबंधित प्रश्न
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
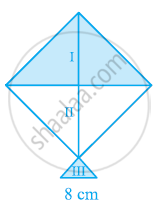
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangles of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it?
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Area of PQRS = Area of PQR + Area of ΔPQS = (6+9.166)𝑐𝑚2=15.166𝑐𝑚2
Find the area of a quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90° and BCD forms an equilateral triangle whose each side is equal to 26 cm. (Take √3 = 1.73)
The sides of a triangle are 11 m, 60 m and 61 m. The altitude to the smallest side is
In the given figure, the ratio AD to DC is 3 to 2. If the area of Δ ABC is 40 cm2, what is the area of Δ BDC?
If every side of a triangle is doubled, then increase in the area of the triangle is
A park is in the shape of a quadrilateral. The sides of the park are 15 m, 20 m, 26 m and 17 m and the angle between the first two sides is a right angle. Find the area of the park
The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is ______.
