Advertisements
Advertisements
प्रश्न
The sides of a quadrilateral, taken in order are 5, 12, 14 and 15 meters respectively, and the angle contained by the first two sides is a right angle. Find its are
उत्तर
Given that sides of quadrilateral are AB = 5 m, BC = 12 m, CD = 14 m and DA = 15 m
AB = 5m, BC = 12m, CD = 14 m and DA = 15 m
Join AC
Area of ΔABC = `1/2`×𝐴𝐵×𝐵𝐶 [∵𝐴𝑟𝑒𝑎 𝑜𝑓 Δ𝑙𝑒=`1/2`(3𝑥+1)]
= `1/2×5×12`
= 30 cm2
In ΔABC By applying Pythagoras theorem.
`AC^2=AB^2+BC^2`
`⇒AC=sqrt(5^2+12^2)`
`⇒sqrt(25+144)`
`⇒sqrt169=13m`
𝑁𝑜𝑤 𝑖𝑛 Δ𝐴𝐷𝐶
Let 2s be the perimeter
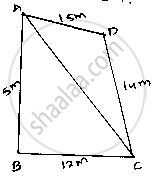
∴ 2s = (AD + DC + AC)
⇒ S = `1/2`(15+14+13)=`1/2`×42=21𝑚
By using Heron’s formula
∴ Area of ΔADC = `sqrt(S(S-AD)(S-DC)(S-AC))`
`=sqrt(21(21-15)(21-14)(21-13))`
`sqrt(21xx6xx7xx8)`
∴𝐴𝑟𝑒𝑎 𝑜𝑓 𝑞𝑢𝑎𝑑𝑟𝑖𝑙𝑎𝑡𝑒𝑟𝑎𝑙 𝐴𝐵𝐶𝐷=𝑎𝑟𝑒𝑎 𝑜𝑓 (Δ𝐴𝐵𝐶)+𝐴𝑟𝑒𝑎 𝑜𝑓 (Δ𝐴𝐷𝐶) = 30 + 84 = `114 m^2`
APPEARS IN
संबंधित प्रश्न
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
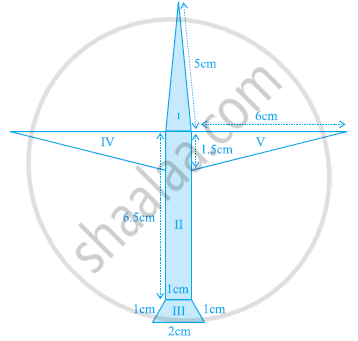
Radha made a picture of an aeroplane with coloured papers as shown in the given figure. Find the total area of the paper used.
Find the area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m.
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD =9 cm, CD = l2cm, ∠ACB = 90° and AC=l5cm.
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
The sides of a triangular field are 325 m, 300 m and 125 m. Its area is
The sides of a triangle are 50 cm, 78 cm and 112 cm. The smallest altitude is
If the area of an isosceles right triangle is 8 cm2, what is the perimeter of the triangle?
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is \[12\sqrt{2}\] cm, then area of the triangle is
The perimeter of an equilateral triangle is 60 m. The area is ______.
