Advertisements
Advertisements
Question
The sides of a quadrilateral, taken in order are 5, 12, 14 and 15 meters respectively, and the angle contained by the first two sides is a right angle. Find its are
Solution
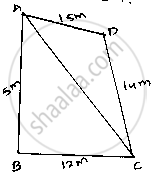
Given that sides of quadrilateral are AB = 5 m, BC = 12 m, CD = 14 m and DA = 15 m
AB = 5m, BC = 12m, CD = 14 m and DA = 15 m
Join AC
Area of ΔABC = `1/2`×๐ด๐ต×๐ต๐ถ [โต๐ด๐๐๐ ๐๐ Δ๐๐=`1/2`(3๐ฅ+1)]
= `1/2×5×12`
= 30 cm2
In ΔABC By applying Pythagoras theorem.
`AC^2=AB^2+BC^2`
`⇒AC=sqrt(5^2+12^2)`
`⇒sqrt(25+144)`
`⇒sqrt169=13m`
๐๐๐ค ๐๐ Δ๐ด๐ท๐ถ
Let 2s be the perimeter
∴ 2s = (AD + DC + AC)
⇒ S = `1/2`(15+14+13)=`1/2`×42=21๐
By using Heron’s formula
∴ Area of ΔADC = `sqrt(S(S-AD)(S-DC)(S-AC))`
`=sqrt(21(21-15)(21-14)(21-13))`
`sqrt(21xx6xx7xx8)`
∴๐ด๐๐๐ ๐๐ ๐๐ข๐๐๐๐๐๐๐ก๐๐๐๐ ๐ด๐ต๐ถ๐ท=๐๐๐๐ ๐๐ (Δ๐ด๐ต๐ถ)+๐ด๐๐๐ ๐๐ (Δ๐ด๐ท๐ถ) = 30 + 84 = `114 m^2`
APPEARS IN
RELATED QUESTIONS
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
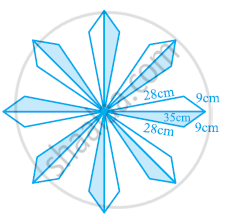
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50p per cm2.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
Let Δ be the area of a triangle. Find the area of a triangle whose each side is twice the side of the given triangle.
The sides of a triangle are 11 cm, 15 cm and 16 cm. The altitude to the largest side is
If the area of an isosceles right triangle is 8 cm2, what is the perimeter of the triangle?
A park is in the shape of a quadrilateral. The sides of the park are 15 m, 20 m, 26 m and 17 m and the angle between the first two sides is a right angle. Find the area of the park
The adjacent sides of a parallelogram measures 34 m, 20 m and the measure of the diagonal is 42 m. Find the area of parallelogram
If the area of an equilateral triangle is `16sqrt(3)` cm2, then the perimeter of the triangle is ______.
