Advertisements
Advertisements
Question
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50p per cm2.
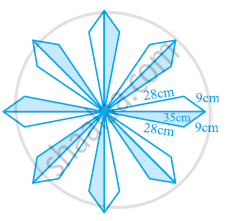
Solution
It can be observed that
Semi-perimeter of each triangular-shaped tile,
`s=(35+28+9)/2=36cm`
By Heron’s formula,
`"Area of triangle "=sqrt(s(s-a)(s-b)(s-c))`
`"Area of each tile "=[sqrt(36(36-35)(36-28)(36-9))]cm^2`
`=[sqrt(36xx1xx8xx27)]cm^2`
`=36sqrt6 cm^2`
= (36 x 2.45) cm^2
= 88.2 cm2
Area of 16 tiles = (16 × 88.2) cm2= 1411.2 cm2
Cost of polishing per cm2 area = 50 p
Cost of polishing 1411.2 cm2 area = Rs (1411.2 × 0.50) = Rs 705.60
Therefore, it will cost Rs 705.60 while polishing all the tiles.
APPEARS IN
RELATED QUESTIONS
Find the area of a quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90° and BCD forms an equilateral triangle whose each side is equal to 26 cm. (Take √3 = 1.73)
Find the area of an equilateral triangle having each side 4 cm.
Let Δ be the area of a triangle. Find the area of a triangle whose each side is twice the side of the given triangle.
If each side of a equilateral triangle is tripled then what is the percentage increase in the area of the triangle?
The base and hypotenuse of a right triangle are respectively 5 cm and 13 cm long. Its area is
If the area of an isosceles right triangle is 8 cm2, what is the perimeter of the triangle?
The lengths of the sides of Δ ABC are consecutive integers. It Δ ABC has the same perimeter as an equilateral triangle with a side of length 9 cm, what is the length of the shortest side of ΔABC?
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is \[12\sqrt{2}\] cm, then area of the triangle is
A land is in the shape of rhombus. The perimeter of the land is 160 m and one of the diagonal is 48 m. Find the area of the land.
The perimeter of an equilateral triangle is 60 m. The area is ______.
