Advertisements
Advertisements
Question
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangles of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it?
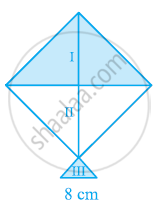
Solution
We know that
Area of square = 1/2(diagonal)2
`"Area of the given kite "= 1/2(32 cm)^2 = 512 cm^2`
Area of 1st shade = Area of 2nd shade = 512/2 = 256 cm2
Therefore, the area of paper required in each shape is 256 cm2.
For IIIrd triangle
Semi-perimeter,
`s=(6+6+8)/2=10 cm`
By Heron’s formula,
`"Area of triangle "=sqrt(s(s-a)(s-b)(s-c))`
`"Area of 3rd triangle "=sqrt(10(10-6)(10-6)(10-8))`
`=(sqrt(10xx4xx4xx2))cm^2`
`=(4xx2sqrt5)cm^2`
`=8sqrt5 cm^2`
= (8 x 2.24) cm2
= 17.92 cm2
Area of paper required for IIIrd shade = 17.92 cm2
APPEARS IN
RELATED QUESTIONS
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
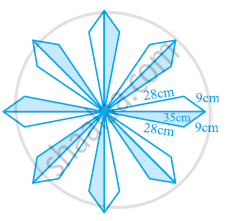
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50p per cm2.
Find the area of an equilateral triangle having each side 4 cm.
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
Mark the correct alternative in each of the following:
The sides of a triangle are 16 cm, 30 cm, 34 cm. Its area is
Find the area of a quadrilateral ABCD whose sides are AB = 13 cm, BC = 12 cm, CD = 9 cm, AD = 14 cm and diagonal BD = 15 cm
The adjacent sides of a parallelogram measures 34 m, 20 m and the measure of the diagonal is 42 m. Find the area of parallelogram
The area of the equilateral triangle is `20sqrt(3)` cm2 whose each side is 8 cm.
In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
