Advertisements
Advertisements
प्रश्न
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangles of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it?
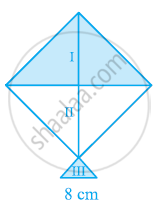
उत्तर
We know that
Area of square = 1/2(diagonal)2
`"Area of the given kite "= 1/2(32 cm)^2 = 512 cm^2`
Area of 1st shade = Area of 2nd shade = 512/2 = 256 cm2
Therefore, the area of paper required in each shape is 256 cm2.
For IIIrd triangle
Semi-perimeter,
`s=(6+6+8)/2=10 cm`
By Heron’s formula,
`"Area of triangle "=sqrt(s(s-a)(s-b)(s-c))`
`"Area of 3rd triangle "=sqrt(10(10-6)(10-6)(10-8))`
`=(sqrt(10xx4xx4xx2))cm^2`
`=(4xx2sqrt5)cm^2`
`=8sqrt5 cm^2`
= (8 x 2.24) cm2
= 17.92 cm2
Area of paper required for IIIrd shade = 17.92 cm2
APPEARS IN
संबंधित प्रश्न
A park, in the shape of a quadrilateral ABCD, has ∠C = 900, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m How much area does it occupy?
Find the area of an equilateral triangle having each side x cm.
If each side of a equilateral triangle is tripled then what is the percentage increase in the area of the triangle?
The sides of a triangle are 11 cm, 15 cm and 16 cm. The altitude to the largest side is
The lengths of the sides of Δ ABC are consecutive integers. It Δ ABC has the same perimeter as an equilateral triangle with a side of length 9 cm, what is the length of the shortest side of ΔABC?
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is \[12\sqrt{2}\] cm, then area of the triangle is
A park is in the shape of a quadrilateral. The sides of the park are 15 m, 20 m, 26 m and 17 m and the angle between the first two sides is a right angle. Find the area of the park
The length of each side of an equilateral triangle having an area of `9sqrt(3)`cm2 is ______.
The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
