Advertisements
Advertisements
प्रश्न
A park, in the shape of a quadrilateral ABCD, has ∠C = 900, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m How much area does it occupy?
उत्तर
Given sides of a quadrilaterals are AB = 9, BC = 12, CD = 05, DA = 08
Let us joint BD
In ΔBCD applying Pythagoras theorem.
`BD^2=BC^2+CD^2`
=`(12)^2+(5)^2`
=144+25
=169
𝐵𝐷=13𝑚
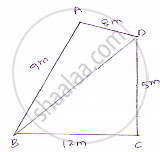
Area of ΔBCD = `1/2`×𝐵𝐶×𝐶𝐷=[`1/2`×12×5]`m^2=30m^2`
or ΔABD
`S=sqrt(perimeter)/2=sqrt(9+8+13)/2=15cm`
By heron’s formula`sqrt(s(s-a)(s-b)(s-c))`
Area of the triangle =`sqrt(15(15-9)(15-8)(15-13))m^2`
=`35.496 + 30 m^2`
= `65.5 m^2` (approximately)
APPEARS IN
संबंधित प्रश्न
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Radha made a picture of an aeroplane with coloured papers as shown in the given figure. Find the total area of the paper used.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Find the area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m.
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
The base of an isosceles right triangle is 30 cm. Its area is
If the area of an isosceles right triangle is 8 cm2, what is the perimeter of the triangle?
The lengths of the sides of Δ ABC are consecutive integers. It Δ ABC has the same perimeter as an equilateral triangle with a side of length 9 cm, what is the length of the shortest side of ΔABC?
The perimeter of an equilateral triangle is 60 m. The area is ______.
The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is ______.
