Advertisements
Advertisements
प्रश्न
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
उत्तर
Let us join BD.
In ΔBCD, applying Pythagoras theorem,
BD2 = BC2 + CD2
= (12)2 + (5)2
= 144 + 25
BD2 = 169
BD = 13 m
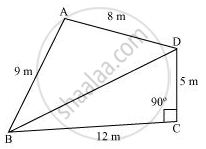
Area of ΔBCD
`= 1/2xxBCxxCD = (1/2xx12xx5)m^2=30m^2`
For ΔABD,
`s="Perimeter"/2=(9+8+12)/2=15m`
By Heron's formula,
`"Area of triangle "=sqrt(s(s-a)(s-b)(s-c))`
`"Area of "triangleABD=[sqrt(15(15-9)(15-8)(15-13))]m^2`
`=(sqrt(15xx6xx7xx2))m^2`
`=6sqrt35 m^2`
= (6 x 5.916) m2
= 35.496 m2
Area of the park = Area of ΔABD + Area of ΔBCD
= 35.496 + 30 m2
= 65.496 m2
= 65.5 m2 (approximately)
APPEARS IN
संबंधित प्रश्न
A triangle and a parallelogram have the same base and the same area. If the sides of triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Area of PQRS = Area of PQR + Area of ΔPQS = (6+9.166)𝑐𝑚2=15.166𝑐𝑚2
The sides of a quadrilateral, taken in order are 5, 12, 14 and 15 meters respectively, and the angle contained by the first two sides is a right angle. Find its are
The perimeter of a triangullar field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
The base and hypotenuse of a right triangle are respectively 5 cm and 13 cm long. Its area is
If the area of an isosceles right triangle is 8 cm2, what is the perimeter of the triangle?
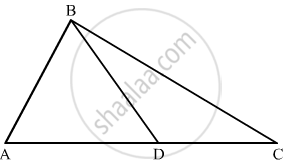
In the given figure, the ratio AD to DC is 3 to 2. If the area of Δ ABC is 40 cm2, what is the area of Δ BDC?
If the length of a median of an equilateral triangle is x cm, then its area is
The length of each side of an equilateral triangle having an area of `9sqrt(3)`cm2 is ______.
The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude ______.
