Advertisements
Advertisements
प्रश्न
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
उत्तर
Let the sides of an isosceles triangle be a = 12 cm, b = 12 cm, c = x cm
Since the perimeter of the triangle = 30 cm
∴ 12 cm + 12 cm + x cm = 30 cm
⇒ x = (30 − 24) = 6
Now, semi-perimeter, s = `30/2` cm = 15 cm
∴ Area of the triangle = `sqrt(s(s - a)(s - b)(s - c))`
= `sqrt(15(15-12)(15-12)(15-6)) cm^2`
= `sqrt(15 xx 3 xx 3 xx 9) cm^2`
= `sqrt(15 xx 3 xx 3 xx 3 xx 3 xx 3) cm^2`
= `sqrt(3^2 xx 3^2 xx 3 xx 5) cm^2`
= `3 xx 3 xx sqrt(3 xx 5) cm^2`
= `9sqrt15 cm^2`
Thus, the required area of the triangle is `9sqrt15 cm^2`.
APPEARS IN
संबंधित प्रश्न
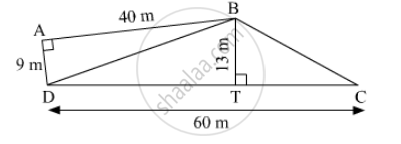
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
Sides of a triangle are cm 45 cm, 39 cm and 42 cm, find its area.
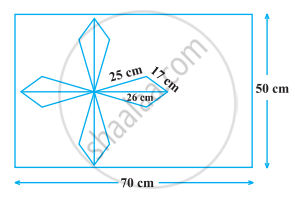
Some measures are given in the adjacent figure, find the area of ☐ABCD.
Determine whether the sets of points are collinear?
(a, b + c), (b, c + a) and (c, a + b)
A man walks near a wall, such that the distance between him and the wall is 10 units. Consider the wall to be the Y-axis. The path travelled by the man is
The perimeter of an equilateral triangle is 30 cm. The area is
The area of the isosceles triangle is `5/4 sqrt(11)` cm2, if the perimeter is 11 cm and the base is 5 cm.
Find the area of a parallelogram given in figure. Also find the length of the altitude from vertex A on the side DC.
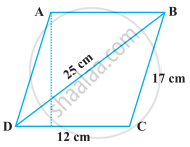
A design is made on a rectangular tile of dimensions 50 cm × 70 cm as shown in the following figure. The design shows 8 triangles, each of sides 26 cm, 17 cm and 25 cm. Find the total area of the design and the remaining area of the tile.