Advertisements
Advertisements
प्रश्न
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
उत्तर
ABC be the triangle, Here a = 78 dm = AB,
BC = b = 50 dm
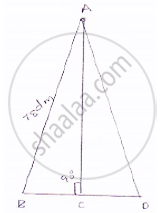
Now, perimeter = 240 dm
⇒ AB + BC + CA = 240 dm
⇒ AC = 240 – BC – AB
⇒ AC = 112 dm
Now, 2s = AB + BC + CA
⇒ 2s = 240
⇒ s = 120 dm
∴ Area of ΔABC =`sqrt(s(s-a)(s-b)(s-b))` by heron's formula
=`sqrt(120(120-78)(120-50)(120-112))`
`=sqrt(120xx42xx70xx8)`
1680 `dm^2`
𝐿𝑒𝑡 𝐴𝐷 𝑏𝑒 𝑝𝑒𝑟𝑝𝑒𝑛𝑑𝑖𝑐𝑢𝑎𝑙𝑎𝑟 𝑜𝑛 𝐵𝐶
Area of ΔABC = `1/2xx ABxxBC `(area of triangle=`(1/2xxbxxh)`
`=1/2xx ADxxBC=1680 `
`⇒AD=(2xx1680)/50=67.2dm`
APPEARS IN
संबंधित प्रश्न
Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
The lengths of the sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side.
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
The area of triangle formed by the points (− 5, 0), (0, – 5) and (5, 0) is
A man walks near a wall, such that the distance between him and the wall is 10 units. Consider the wall to be the Y-axis. The path travelled by the man is
An advertisement board is in the form of an isosceles triangle with perimeter 36 m and each of the equal sides are 13 m. Find the cost of painting it at ₹ 17.50 per square metre.
Find the area of the unshaded region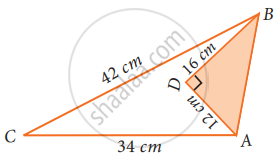
From a point in the interior of an equilateral triangle, perpendiculars are drawn on the three sides. The lengths of the perpendiculars are 14 cm, 10 cm and 6 cm. Find the area of the triangle.
The sides of a quadrilateral ABCD are 6 cm, 8 cm, 12 cm and 14 cm (taken in order) respectively, and the angle between the first two sides is a right angle. Find its area.
