Advertisements
Advertisements
प्रश्न
The perimeter of a triangle is 300 m. If its sides are in the ratio 3 : 5 : 7. Find the area of the triangle ?
उत्तर
Given that
The perimeter of a triangle = 300 m
The sides of a triangle in the ratio 3 : 5 : 7
Let 3x, 5x, 7x be the sides of the triangle
Perimeter ⇒ 2s = a + b + c
⇒ 3x + 5x + 17x = 300
⇒ 15x = 300
⇒ x = 20m
The triangle sides are a = 3x
= 3 (20)m = 60 m
b = 5x = 5(20) m = 100m
c = 7x = 140 m
semi perimeter s = `(a+b+c+)/2`
`=(300)/2m`
`=150m`
∴The area of the triangle `=sqrt(s(s-a)(s-b)(s-c))`
`=sqrt(150(150-60)(150-100)(150-140))`
`=sqrt(150xx10xx90xx50)`
`=sqrt(1500xx1500) 3 cm^2`
`∴Δ` le Area = 1500 `sqrt3 cm^2`
APPEARS IN
संबंधित प्रश्न
A triangle has sides 35 cm, 54 cm and 61 cm long. Find its area. Also, find the smallest of its altitudes ?
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
Some measures are given in the adjacent figure, find the area of ☐ABCD.
Find the area of the triangle formed by the points
(–10, –4), (–8, –1) and (–3, –5)
A man walks near a wall, such that the distance between him and the wall is 10 units. Consider the wall to be the Y-axis. The path travelled by the man is
If (5, 7), (3, p) and (6, 6) are collinear, then the value of p is
Find the area of the unshaded region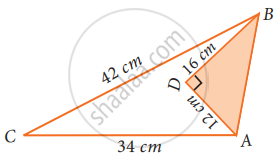
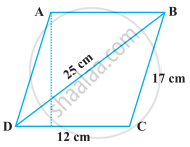
Find the area of a parallelogram given in figure. Also find the length of the altitude from vertex A on the side DC.
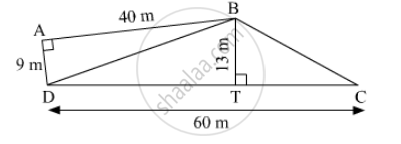
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
