Advertisements
Advertisements
प्रश्न
The perimeter of a triangle is 300 m. If its sides are in the ratio 3 : 5 : 7. Find the area of the triangle ?
उत्तर
Given that
The perimeter of a triangle = 300 m
The sides of a triangle in the ratio 3 : 5 : 7
Let 3x, 5x, 7x be the sides of the triangle
Perimeter ⇒ 2s = a + b + c
⇒ 3x + 5x + 17x = 300
⇒ 15x = 300
⇒ x = 20m
The triangle sides are a = 3x
= 3 (20)m = 60 m
b = 5x = 5(20) m = 100m
c = 7x = 140 m
semi perimeter s = `(a+b+c+)/2`
`=(300)/2m`
`=150m`
∴The area of the triangle `=sqrt(s(s-a)(s-b)(s-c))`
`=sqrt(150(150-60)(150-100)(150-140))`
`=sqrt(150xx10xx90xx50)`
`=sqrt(1500xx1500) 3 cm^2`
`∴Δ` le Area = 1500 `sqrt3 cm^2`
APPEARS IN
संबंधित प्रश्न
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
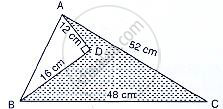
Find the area of the shaded region in the given figure.
Find the area of an isosceles triangle having the base x cm and one side y cm.
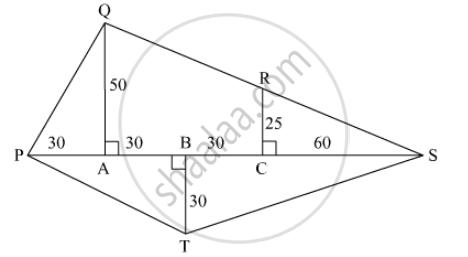
Find the areas of the given plot. (All measures are in metres.)
Determine whether the sets of points are collinear?
`(-1/2, 3), (-5, 6) and (-8, 8)`
Determine whether the sets of points are collinear?
(a, b + c), (b, c + a) and (c, a + b)
The area of triangle formed by the points (− 5, 0), (0, – 5) and (5, 0) is
An advertisement board is in the form of an isosceles triangle with perimeter 36 m and each of the equal sides are 13 m. Find the cost of painting it at ₹ 17.50 per square metre.
The semi-perimeter of a triangle having sides 15 cm, 20 cm and 25 cm is
