Advertisements
Advertisements
प्रश्न
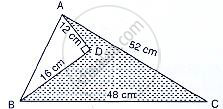
Find the area of the shaded region in the given figure.
उत्तर
We are given the following figure with dimensions.
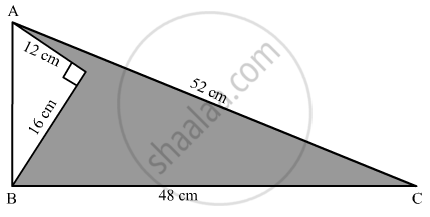
Area of shaded region = Area of ΔABC – Area of ΔADB
Now in ΔADB
`⇒ AB62 = AD^2 + BD^2` --(i)
⇒ Given that AD = 12 cm BD = 16 cm
Substituting the values of AD and BD in the equation (i), we get
`AB^2=12^2+16^2`
`AB^2=144+256`
`AB=sqrt400`
`AB=20cm`
∴ Area of triangle = `1/2xxADxxBD`
`=1/2xx12xx16`
`=96cm^2`
Now
In ΔABC, S =`1/2(AB+BC+CA)`
`=1/2xx(52+48+20)`
`1/2(120)`
`60cm`
By using heron’s formula
We know that, Area of Δle ABC `=sqrt(s(s-a)(s-b)(s-c))`
`=sqrt(60(60-20)(60-48)(60-52))`
`=sqrt(60(40)(12)(8))`
`=480cm^2`
`Area of shaded region = Area of ΔABC – Area of ΔADB`
`=(480-96)cm^2`
`384 cm^2`
∴ Area of shaded region = 384 `cm^2`
APPEARS IN
संबंधित प्रश्न
The perimeter of a triangle is 300 m. If its sides are in the ratio 3 : 5 : 7. Find the area of the triangle ?
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
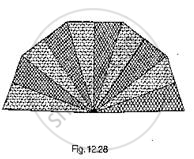
A hand fan is made by stitching lo equal size triangular strips of two different types of paper as shown in Fig. 12.28. The dimensions of equal strips are 25 cm, 25 cm and 14 cm. Find the area of each type of paper needed to make the hand fan.
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
Find the area of a triangle formed by the lines 3x + y – 2 = 0, 5x + 2y – 3 = 0 and 2x – y – 3 = 0
The perimeter of an equilateral triangle is 30 cm. The area is
An isosceles right triangle has area 8 cm2. The length of its hypotenuse is ______.
The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
A field is in the shape of a trapezium having parallel sides 90 m and 30 m. These sides meet the third side at right angles. The length of the fourth side is 100 m. If it costs Rs 4 to plough 1 m2 of the field, find the total cost of ploughing the field.
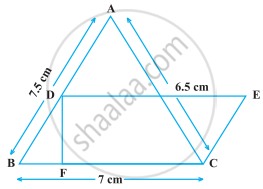
In the following figure, ∆ABC has sides AB = 7.5 cm, AC = 6.5 cm and BC = 7 cm. On base BC a parallelogram DBCE of same area as that of ∆ABC is constructed. Find the height DF of the parallelogram.