Advertisements
Advertisements
प्रश्न
Find the area of a triangle formed by the lines 3x + y – 2 = 0, 5x + 2y – 3 = 0 and 2x – y – 3 = 0
उत्तर
3x + y = 2 ...(1)
5x + 2y = 3 ...(2)
2x – y = 3 ...(3)
Solve (1) and (2) to get the vertices B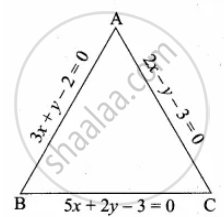
(1) × 2 ⇒ 6x + 2y = 4 ...(1)
(1) × 2 ⇒ 5x + 2y = 3 ...(2)
(−) (−) (−)
Subtract (1) and (2) ⇒ x = 1
Substitute the value of x = 1 in (1)
3(1) + y = 2
y = 2 – 3 = – 1
The point B is (1, – 1)
Solve (2) and (3) to get the vertices C
(2) × 1 ⇒ 5x + 2y = 3 ...(2)
(3) × 2 ⇒ 4x – 2y = 6 ...(4)
Adding (2) and (4) ⇒ 9x = 9
x = 1
Substitute the value of x = 1 in (3)
2(1) – y = 3
⇒ – y = 3 – 2
– y = 1
⇒ y = – 1
The point C is (1, – 1)
Solve (1) and (3) to get the vertices A
3x + y = 2 ...(1)
2x – 2y = 3 ...(2)
By adding (1) and (2) ⇒ 5x = 5
Substitute the value of x = 1 in (1)
3(1) + y = 2
y = 2 – 3 = – 1
The point A is (1, – 1)
The points A (1, – 1), B (1, – 1), C(1, – 1)
Area of ∆ABC = `1/2[x_1y_2 + x_2y_3 + x_3y_1 - (x_2y_1 + x_3y_2 + x_1y_3)]`
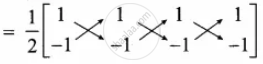
= `1/2 [-1 + (- 1)+ (- 1) - (- 1 + (- 1) + (- 1))]`
= `1/2[-3 - (- 3)]`
= `1/2[- 3 + 3]`
= `1/2 xx 0` = 0
Area of the triangle = 0 sq. units.
APPEARS IN
संबंधित प्रश्न
Find the area of an isosceles triangle having the base x cm and one side y cm.
Find the areas of the given plot. (All measures are in metres.)
A triangular shaped glass with vertices at A(– 5, – 4), B(1, 6) and C(7, – 4) has to be painted. If one bucket of paint covers 6 square feet, how many buckets of paint will be required to paint the whole glass, if only one coat of paint is applied
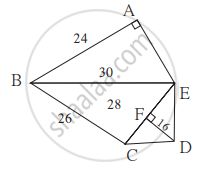
Find the area of triangle AGF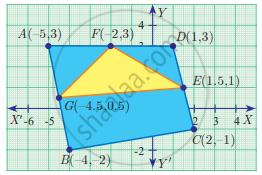
A man walks near a wall, such that the distance between him and the wall is 10 units. Consider the wall to be the Y-axis. The path travelled by the man is
An advertisement board is in the form of an isosceles triangle with perimeter 36 m and each of the equal sides are 13 m. Find the cost of painting it at ₹ 17.50 per square metre.
The area of the isosceles triangle is `5/4 sqrt(11)` cm2, if the perimeter is 11 cm and the base is 5 cm.
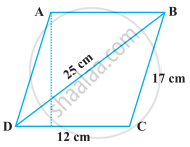
Find the area of a parallelogram given in figure. Also find the length of the altitude from vertex A on the side DC.
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
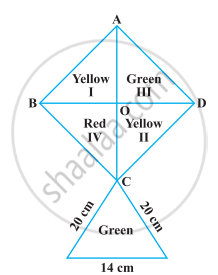
How much paper of each shade is needed to make a kite given in the following figure, in which ABCD is a square with diagonal 44 cm.