Advertisements
Advertisements
प्रश्न
The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (3, −2). The third vertex is (x, y) where y = x + 3. Find the coordinates of the third vertex.
उत्तर
Let the vertices A(2, 1), B(3, –2) and C(x, y)
Area of a triangle = 5 sq. units
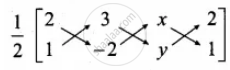
`1/2[x_1y_2 + x_2y_3 + x_3y_1 - (x_2y_1 + x_3y_2 + x_1y_3)]` = 5
`1/2[- 4 + 3y + x - (3 - 2x + 2y)]` = 5
– 4 + 3y + x – 3 + 2x – 2y = 10
3x + y – 7 = 10
3x + y = 17 ...(1)
Given y = x + 3
Substitute the value ofy = x + 3 in (1)
3x + x + 3 = 17
4x = 17 – 3
4x = 14
x = `14/4 = 7/2`
Substitute the value of x in y = x + 3
y = `7/2 + 3`
⇒ y = `(7 + 6)/2`
= `13/2`
∴ The coordinates of the third vertex is `(7/2, 13/2)`
APPEARS IN
संबंधित प्रश्न
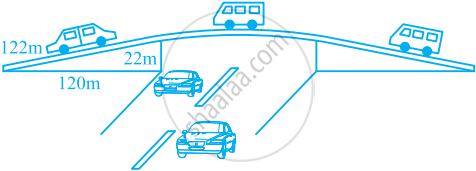
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122m, 22m, and 120m (see the given figure). The advertisements yield an earning of ₹ 5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
Find the area of a triangle whose sides are 3 cm, 4 cm and 5 cm respectively.
Find the area of an isosceles triangle having the base x cm and one side y cm.
Find the areas of the given plot. (All measures are in metres.)
A triangular shaped glass with vertices at A(– 5, – 4), B(1, 6) and C(7, – 4) has to be painted. If one bucket of paint covers 6 square feet, how many buckets of paint will be required to paint the whole glass, if only one coat of paint is applied
A man walks near a wall, such that the distance between him and the wall is 10 units. Consider the wall to be the Y-axis. The path travelled by the man is
The perimeter of a triangular plot is 600 m. If the sides are in the ratio 5 : 12 : 13, then find the area of the plot
The sides of a quadrilateral ABCD are 6 cm, 8 cm, 12 cm and 14 cm (taken in order) respectively, and the angle between the first two sides is a right angle. Find its area.
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
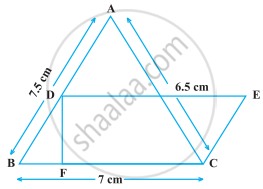
In the following figure, ∆ABC has sides AB = 7.5 cm, AC = 6.5 cm and BC = 7 cm. On base BC a parallelogram DBCE of same area as that of ∆ABC is constructed. Find the height DF of the parallelogram.