Advertisements
Advertisements
प्रश्न
Find the area of a triangle whose sides are 3 cm, 4 cm and 5 cm respectively.
उत्तर
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
`A = sqrt( s(s-a)(s-b)(s-c)`, where
`s = (a+b+c)/2`
Therefore the area of a triangle, say having sides 3 cm, 4 cm and 5 cm is given by
a = 3 cm ; b = 4 cm ; c = 5 cm
`s = (a+b+c)/2`
`s = (3+4+5)/2`
`s =12/2`
s = 6 cm Now, area `A = sqrt(s(s-a)(s-b)(s-c)`
\[= \sqrt{6(6 - 3)(6 - 4)(6 - 5)}\]
\[ = \sqrt{6 \times 3 \times 2 \times 1}\]
\[ = \sqrt{36}\]
\[ = 6 c m^2\]
APPEARS IN
संबंधित प्रश्न
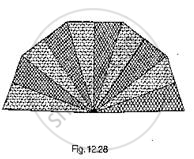
A hand fan is made by stitching lo equal size triangular strips of two different types of paper as shown in Fig. 12.28. The dimensions of equal strips are 25 cm, 25 cm and 14 cm. Find the area of each type of paper needed to make the hand fan.
Sides of a triangle are cm 45 cm, 39 cm and 42 cm, find its area.
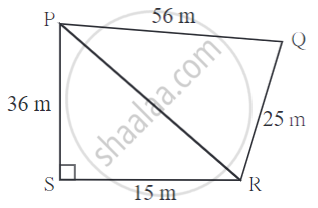
Look at the measures shown in the adjacent figure and find the area of ☐ PQRS.
Find the area of triangle AGF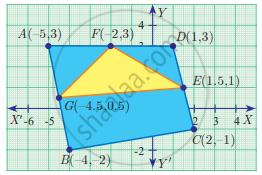
The area of triangle formed by the points (− 5, 0), (0, – 5) and (5, 0) is
A man walks near a wall, such that the distance between him and the wall is 10 units. Consider the wall to be the Y-axis. The path travelled by the man is
The perimeter of a triangular plot is 600 m. If the sides are in the ratio 5 : 12 : 13, then find the area of the plot
The area of the isosceles triangle is `5/4 sqrt(11)` cm2, if the perimeter is 11 cm and the base is 5 cm.
The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
The sides of a quadrilateral ABCD are 6 cm, 8 cm, 12 cm and 14 cm (taken in order) respectively, and the angle between the first two sides is a right angle. Find its area.
