Advertisements
Advertisements
प्रश्न
The sides of a quadrilateral ABCD are 6 cm, 8 cm, 12 cm and 14 cm (taken in order) respectively, and the angle between the first two sides is a right angle. Find its area.
उत्तर
Given ABCD is a quadrilateral having sides AB = 6 cm, BC = 8 cm, CD = 12 cm and DA = 14 cm.
Now, join AC.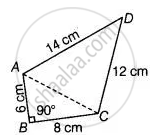
We have, ABC is a right-angled triangled at B.
Now, AC2 = AB2 + BC2 ...[By Pythagoras theorem]
= 62 + 82
= 36 + 64
= 100
⇒ AC = 10 cm ...[Taking positive square root]
∴ Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD ...(i)
Now, area of ΔABC = `1/2 xx AB xx BC` ...[∵ Area of triangle = `1/2` (base × height)]
= `1/2 xx 6 xx 8`
= 24 cm2
In ΔACD, AC = a = 10 cm, CD = b = 12 cm
And DA = c = 14 cm
Now, semi-perimeter of ΔACD,
`s = (a + b + c)/2`
= `(10 + 12 + 14)/2`
= `36/2`
= 18 cm
Area of ΔACD = `sqrt(s(s - a)(s - b)(s - c))` ...[By Heron’s formula]
= `sqrt(18(18 - 10)(18 - 12)(18 - 14))`
= `sqrt(18 xx 8 xx 6 xx 4)`
= `sqrt((3)^2 xx 2 xx 4 xx 2 xx 3 xx 2 xx 4)`
= `3 xx 4 xx 2 sqrt(3 xx 2)`
= `24sqrt(6) cm^2`
From equation (i),
Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD
= `24 + 24sqrt(6)`
= `24(1 + sqrt(6)) cm^2`
Hence, the area of quadrilateral is `24(1 + sqrt(6)) cm^2`.
APPEARS IN
संबंधित प्रश्न
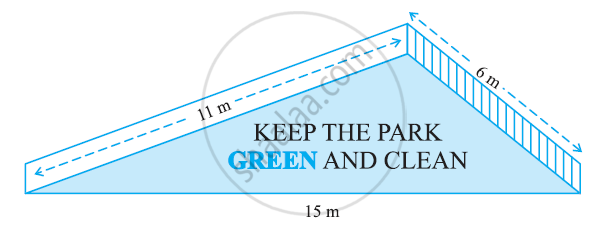
There is a slide in the park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see the given figure). If the sides of the wall are 15m, 11m, and 6m, find the area painted in colour.
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
The perimeter of an isosceles triangle is 42 cm and its baše is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
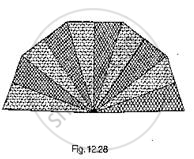
A hand fan is made by stitching lo equal size triangular strips of two different types of paper as shown in Fig. 12.28. The dimensions of equal strips are 25 cm, 25 cm and 14 cm. Find the area of each type of paper needed to make the hand fan.
Using Heron’s formula, find the area of a triangle whose sides are 1.8 m, 8 m, 8.2 m
The perimeter of a triangular plot is 600 m. If the sides are in the ratio 5 : 12 : 13, then find the area of the plot
An advertisement board is in the form of an isosceles triangle with perimeter 36 m and each of the equal sides are 13 m. Find the cost of painting it at ₹ 17.50 per square metre.
The semi-perimeter of a triangle having sides 15 cm, 20 cm and 25 cm is
The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
