Advertisements
Advertisements
प्रश्न
The sides of a quadrilateral ABCD are 6 cm, 8 cm, 12 cm and 14 cm (taken in order) respectively, and the angle between the first two sides is a right angle. Find its area.
उत्तर
Given ABCD is a quadrilateral having sides AB = 6 cm, BC = 8 cm, CD = 12 cm and DA = 14 cm.
Now, join AC.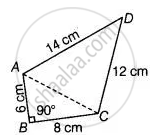
We have, ABC is a right-angled triangled at B.
Now, AC2 = AB2 + BC2 ...[By Pythagoras theorem]
= 62 + 82
= 36 + 64
= 100
⇒ AC = 10 cm ...[Taking positive square root]
∴ Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD ...(i)
Now, area of ΔABC = `1/2 xx AB xx BC` ...[∵ Area of triangle = `1/2` (base × height)]
= `1/2 xx 6 xx 8`
= 24 cm2
In ΔACD, AC = a = 10 cm, CD = b = 12 cm
And DA = c = 14 cm
Now, semi-perimeter of ΔACD,
`s = (a + b + c)/2`
= `(10 + 12 + 14)/2`
= `36/2`
= 18 cm
Area of ΔACD = `sqrt(s(s - a)(s - b)(s - c))` ...[By Heron’s formula]
= `sqrt(18(18 - 10)(18 - 12)(18 - 14))`
= `sqrt(18 xx 8 xx 6 xx 4)`
= `sqrt((3)^2 xx 2 xx 4 xx 2 xx 3 xx 2 xx 4)`
= `3 xx 4 xx 2 sqrt(3 xx 2)`
= `24sqrt(6) cm^2`
From equation (i),
Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD
= `24 + 24sqrt(6)`
= `24(1 + sqrt(6)) cm^2`
Hence, the area of quadrilateral is `24(1 + sqrt(6)) cm^2`.
APPEARS IN
संबंधित प्रश्न
Find the area of the shaded region in the given figure.
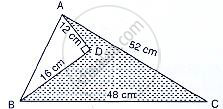
Sides of a triangle are cm 45 cm, 39 cm and 42 cm, find its area.
Find the area of the triangle formed by the points
(1, – 1), (– 4, 6) and (– 3, – 5)
Find the area of triangle AGF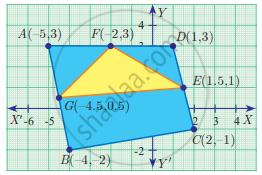
Find the area of a triangle formed by the lines 3x + y – 2 = 0, 5x + 2y – 3 = 0 and 2x – y – 3 = 0
Using Heron’s formula, find the area of a triangle whose sides are 10 cm, 24 cm, 26 cm
The perimeter of an equilateral triangle is 30 cm. The area is
The area of the isosceles triangle is `5/4 sqrt(11)` cm2, if the perimeter is 11 cm and the base is 5 cm.
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
