Advertisements
Advertisements
प्रश्न
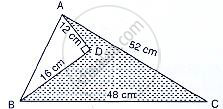
Find the area of the shaded region in the given figure.
उत्तर
We are given the following figure with dimensions.
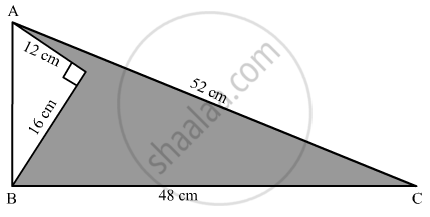
Area of shaded region = Area of ΔABC – Area of ΔADB
Now in ΔADB
`⇒ AB62 = AD^2 + BD^2` --(i)
⇒ Given that AD = 12 cm BD = 16 cm
Substituting the values of AD and BD in the equation (i), we get
`AB^2=12^2+16^2`
`AB^2=144+256`
`AB=sqrt400`
`AB=20cm`
∴ Area of triangle = `1/2xxADxxBD`
`=1/2xx12xx16`
`=96cm^2`
Now
In ΔABC, S =`1/2(AB+BC+CA)`
`=1/2xx(52+48+20)`
`1/2(120)`
`60cm`
By using heron’s formula
We know that, Area of Δle ABC `=sqrt(s(s-a)(s-b)(s-c))`
`=sqrt(60(60-20)(60-48)(60-52))`
`=sqrt(60(40)(12)(8))`
`=480cm^2`
`Area of shaded region = Area of ΔABC – Area of ΔADB`
`=(480-96)cm^2`
`384 cm^2`
∴ Area of shaded region = 384 `cm^2`
APPEARS IN
संबंधित प्रश्न
The perimeter of an isosceles triangle is 42 cm and its baše is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
Sides of a triangle are cm 45 cm, 39 cm and 42 cm, find its area.
Find the areas of the given plot. (All measures are in metres.)
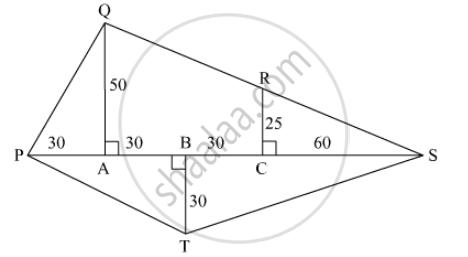
Find the areas of the given plot. (All measures are in metres.)
A triangular shaped glass with vertices at A(– 5, – 4), B(1, 6) and C(7, – 4) has to be painted. If one bucket of paint covers 6 square feet, how many buckets of paint will be required to paint the whole glass, if only one coat of paint is applied
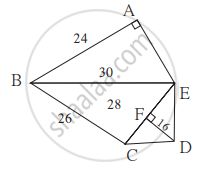
Find the area of triangle FED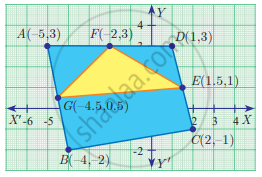
Find the area of an equilateral triangle whose perimeter is 180 cm
The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
A field is in the shape of a trapezium having parallel sides 90 m and 30 m. These sides meet the third side at right angles. The length of the fourth side is 100 m. If it costs Rs 4 to plough 1 m2 of the field, find the total cost of ploughing the field.
