Advertisements
Advertisements
प्रश्न
The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
उत्तर
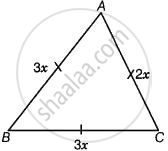
Let ABC be an isosceles triangle with perimeter 32 cm.
We have, ratio of equal side to its base is 3 : 2.
Let sides of triangle be AB = AC = 3x, BC = 2x
∵ Perimeter of a triangle = 32 m
Now, 3x + 3x + 2x = 32
`\implies` 8x = 32
`\implies` x = 4
∴ AB = AC = 3 × 4 = 12 cm
And BC = 2x = 2 × 4 = 8 cm
The sides of a triangle are a = 12 cm, b = 12 cm and c = 8 cm.
∴ Semi-perimeter of an isosceles triangle,
`s = (a + b + c)/2`
= `(12 + 12 + 8)/2`
= `32/2`
= 16 cm
∴ Area of an isosceles ΔABC
= `sqrt(s(s - a)(s - b)(s - c))` ...[By Heron’s formula]
= `sqrt(16(16 - 12)(16 - 12)(16 - 8))`
= `sqrt(16 xx 4 xx 4 xx 8)`
= `4 xx 4 xx 2sqrt(2) cm^2`
= `32sqrt(2) cm^2`
Hence, the area of an isosceles triangle is `32sqrt(2) cm^2`.
APPEARS IN
संबंधित प्रश्न
The perimeter of an isosceles triangle is 42 cm and its baše is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
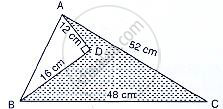
Find the area of the shaded region in the given figure.
Find the area of a triangle whose sides are 3 cm, 4 cm and 5 cm respectively.
Find the area of an isosceles triangle having the base x cm and one side y cm.
Find the areas of the given plot. (All measures are in metres.)
The area of triangle formed by the points (− 5, 0), (0, – 5) and (5, 0) is
Find the area of a triangle formed by the lines 3x + y – 2 = 0, 5x + 2y – 3 = 0 and 2x – y – 3 = 0
The cost of levelling the ground in the form of a triangle having the sides 51 m, 37 m and 20 m at the rate of Rs 3 per m2 is Rs 918.
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
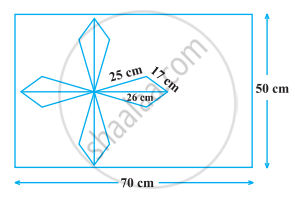
A design is made on a rectangular tile of dimensions 50 cm × 70 cm as shown in the following figure. The design shows 8 triangles, each of sides 26 cm, 17 cm and 25 cm. Find the total area of the design and the remaining area of the tile.