Advertisements
Advertisements
Question
The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
Solution
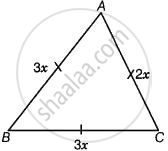
Let ABC be an isosceles triangle with perimeter 32 cm.
We have, ratio of equal side to its base is 3 : 2.
Let sides of triangle be AB = AC = 3x, BC = 2x
∵ Perimeter of a triangle = 32 m
Now, 3x + 3x + 2x = 32
`\implies` 8x = 32
`\implies` x = 4
∴ AB = AC = 3 × 4 = 12 cm
And BC = 2x = 2 × 4 = 8 cm
The sides of a triangle are a = 12 cm, b = 12 cm and c = 8 cm.
∴ Semi-perimeter of an isosceles triangle,
`s = (a + b + c)/2`
= `(12 + 12 + 8)/2`
= `32/2`
= 16 cm
∴ Area of an isosceles ΔABC
= `sqrt(s(s - a)(s - b)(s - c))` ...[By Heron’s formula]
= `sqrt(16(16 - 12)(16 - 12)(16 - 8))`
= `sqrt(16 xx 4 xx 4 xx 8)`
= `4 xx 4 xx 2sqrt(2) cm^2`
= `32sqrt(2) cm^2`
Hence, the area of an isosceles triangle is `32sqrt(2) cm^2`.
APPEARS IN
RELATED QUESTIONS
The lengths of the sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side.
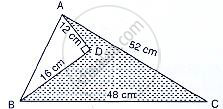
Find the area of the shaded region in the given figure.
A rhombus sheet, whose perimeter is 32 m and whose one diagonal is 10 m long, is painted on both sides at the rate of Rs 5 per m2. Find the cost of painting.
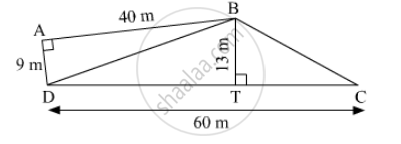
Some measures are given in the adjacent figure, find the area of ☐ABCD.
Find the area of the triangle formed by the points
(–10, –4), (–8, –1) and (–3, –5)
Find the area of triangle FED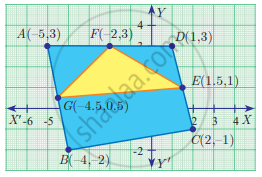
The area of triangle formed by the points (− 5, 0), (0, – 5) and (5, 0) is
A man walks near a wall, such that the distance between him and the wall is 10 units. Consider the wall to be the Y-axis. The path travelled by the man is
An advertisement board is in the form of an isosceles triangle with perimeter 36 m and each of the equal sides are 13 m. Find the cost of painting it at ₹ 17.50 per square metre.
From a point in the interior of an equilateral triangle, perpendiculars are drawn on the three sides. The lengths of the perpendiculars are 14 cm, 10 cm and 6 cm. Find the area of the triangle.
